Задача №1. Мастер обслуживает 5 станков. 20% рабочего времени он проводит у первого станка, 10% - у второго, 15% - у третьего, 25% - у четвертого, 30% - у пятого станка. Найти вероятность того, что в наудачу выбранный момент времени мастер находится:
а) у второго или четвертого станка;
б) у первого, или второго, или третьего станка;
в) не у пятого станка.
Решение. Рассмотрим события:  - в наудачу выбранный момент времени мастер находится соответственно у первого, у второго, у третьего, у четвертого, у пятого станка.
- в наудачу выбранный момент времени мастер находится соответственно у первого, у второго, у третьего, у четвертого, у пятого станка.
Рассмотрим также события  , состоящие в том, что в наудачу выбранный момент времени мастер находится соответственно:
, состоящие в том, что в наудачу выбранный момент времени мастер находится соответственно:
А - у второго или четвертого станка;
В - у первого, второго или третьего станка;
С - не у пятого станка.
Вероятности событий  согласно формуле (1), равны:
согласно формуле (1), равны: 
 - несовместные события, составляющие полную группу.
- несовместные события, составляющие полную группу.
а) Событие А равно сумме несовместных событий  и
и 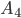 :
:  . Вероятность события А найдем по формуле (8):
. Вероятность события А найдем по формуле (8):

б) Событие В состоит в том, что в наудачу выбранный момент времени мастер находится или у первого, или у второго, или у третьего станка (безразлично, у какого из этих трех указанных). Это означает, что В представляет собой сумму трех несовместных событий
 ,
,  и
и 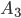 :
:  .
.Вероятность события B найдем по формуле (9):

в) Событие С противоположно событию
 :
:  .
.Вероятность события
 найдем по формуле (11):
найдем по формуле (11):
Задача №2. При определении гранулометрического состава почв было выявлено, что среди 12 образцов имеются 3 образца супесчаной, 4 - глинистой и 5 образцов суглинистой почвы. Найти вероятность того, что два определенных образца (например, помеченные номерами 1 и 2) при классификации по гранулометрическому составу могут быть отнесены к одной и той же группе.
Решение. Пусть взяли 2 определенных образца из 12 имеющихся. Рассмотрим события:
 - взяли 2 образца супесчаной почвы;
- взяли 2 образца супесчаной почвы;
 - взяли 2 образца глинистой почвы;
- взяли 2 образца глинистой почвы;
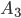 - взяли 2 образца суглинистой почвы;
- взяли 2 образца суглинистой почвы;
 - взяли 2 образца, которые могут быть отнесены к одной и той же группе гранулометрического состава.
- взяли 2 образца, которые могут быть отнесены к одной и той же группе гранулометрического состава.
 ,
,  и
и 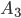 - несовместные события. Событие А наступит, если образцы будут или оба супесчаные, или оба глинистые, или оба суглинистые. Это означает, что событие А является суммой трех несовместных событий
- несовместные события. Событие А наступит, если образцы будут или оба супесчаные, или оба глинистые, или оба суглинистые. Это означает, что событие А является суммой трех несовместных событий  ,
,  и
и 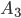 :
:  .
.
Вероятность события А найдем по теореме сложения вероятностей нескольких несовместных событий, в соответствии с формулой (9) при n = 3 получим:

Каждое из слагаемых
 найдем по формуле (1):
найдем по формуле (1):
Числа
 определим по формулам теории соединений.
определим по формулам теории соединений.Всего имеется 12 образцов - 12 элементов. В каждое соединение входят 2 элемента, соединения отличаются друг от друга хотя бы одним элементом, причем порядок элементов роли не играет. Следовательно, рассматриваемые соединения представляют собой сочетания. Найдем
 , применяя формулу (4):
, применяя формулу (4):
Вероятности событий
 ,
,  и
и 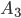 равны:
равны:
Вероятность события А равна









