Решение задач на сложение и умножение вероятностей. Часть 3

Задача №1. Имеются 14 таблиц, содержащих данные о влажности на различной глубине тяжелосуглинистой черноземной почвы. В шести из этих таблиц приведены данные, полученные методом горячей сушки образцов при 105° С, а в остальных - методом холодной сушки над 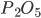$P_{2}O_{5}$ . Какова вероятность того, что среди трех случайным образом отобранных таблиц хотя бы одна таблица содержит данные, полученные методом горячей сушки?
Решение. Отнесем таблицы, содержащие данные, полученные методом горячей сушки, к группе 1, а методом холодной сушки - к группе 2.
Первый способ. Известно, что случайным образом отобраны З таблицы. Рассмотрим события:
В - отобраны одна таблица группы 1 и две таблицы группы 2;
С - отобраны две таблицы группы 1 и одна таблица группы 1;
D - отобраны три таблицы группы 1;
А - отобрана хотя бы одна таблица группы 1.
События B, С и D несовместны. Событие А наступит, если среди трех отобранных таблиц будут находиться или одна, или две, или три таблицы группы 1. Это означает, что событие А является суммой трех несовместных событий В, С и D: A=B+C+D.
Найдем вероятность события А, применив теорему сложения вероятностей несовместных событий. Воспользовавшись формулой (9), получим:

$P(A)=P(B+C+D)=P(B)+P(C)+P(D).\; \; \; (*)$

Вероятности событий B, С и D равны:

$P(B)=\frac{C_{6}^{1}\cdot C_{8}^{2}}{C_{14}^{3}}=\frac{42}{91},\; P(C)=\frac{C_{6}^{2}\cdot C_{8}^{1}}{C_{14}^{3}}=\frac{30}{91},\; P(D)=\frac{C_{6}^{3}}{C_{14}^{3}}=\frac{5}{91}.$

Подставив эти значения в равенство (*), получим

$P(A)=\frac{42}{91}+\frac{30}{91}+\frac{5}{91}=\frac{11}{13}.$

Второй способ. Рассмотрим события:

$A$ - отобрана хотя бы одна таблица группы 1;

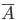$\bar{A}$ - не отобрано ни одной таблицы группы 1, то есть отобрано три таблицы группы 2.

$A$ и

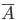$\bar{A}$ - противоположные события, поэтому

$P(A)=1-P(\bar{A})$ .
Вероятность события

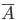$\bar{A}$ равна

$P(A)=\frac{C_{8}^{3}}{C_{14}^{3}}=\frac{2}{13}.$

Искомая вероятность

$P(A)=1-P(\bar{A})=1-\frac{2}{13}=\frac{11}{13}.$

Замечание. Сравнив оба способа решения задачи, видим, что второй способ является более рациональным.
Если в задаче требуется найти вероятность события

$A$ - "получение хотя бы одного нужного результата", то целесообразно вначале рассмотреть противоположное ему событие. Событию

$A$ противоположно событию

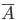$\bar{A}$ - "не получение ни одного нужного результата". Вычислив

$P(\bar{A})$ , найдем затем вероятность

$P(A)$ так:

$P(A)=1-P(\bar{A})$ .

Задача №2. В отделе зеленого чеpeнкoвaния плодовой опытной станции для посадки в теплице подготовили 20 зеленых черенков, среди которых 8 черенков зимостойкой алычи сорта 9-114, а остальные - черенки сливы сорта Евразия 21. Случайным образом отобрано 3 черенка. Найти вероятность того, что хотя бы один из них является черенком алычи.
Решение. Эта задача такого же типа, как задача 1. Для ее рационального решения рекомендуем применить способ, рассмотренный в задаче 1 вторым.
Рассмотрим события:
$A$ - отобран хотя бы один черенок алычи;
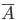$\bar{A}$ - не отобрано ни одного черенка алычи.
Вероятность события 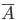$\bar{A}$ равна

$P(\bar{A})=\frac{C_{12}^{3}}{C_{20}^{3}}=\frac{11}{57}.$

Событие

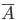$\bar{A}$ противоположно событию

$A$ , поэтому, Согласно формуле (11), искомая вероятность равна

$P(A)=1-P(\bar{A})=1-\frac{11}{57}=\frac{46}{57}\approx 0,8070.$

Задача №3. В кейсе находятся 20 кассет с записями музыки в стиле диско и 10 - в стиле техно. Диджей наудачу берет одну за другой две кассеты. Какова вероятность того, что
1) на первой кассете записана музыка в стиле диско;
2) на второй кассете также записана музыка в стиле диско.
Рассмотреть два случая: перед тем, как взять вторую кассету, диджей
а) возвращает в кейс первую кассету;
б) первую кассету в кейс не возвращает.
Решение. Рассмотрим события:
$A$ - на первой кассете записана музыка в стиле диско;
$B$ - на второй кассете записана музыка в стиле диско.
1) Найдем вероятность события $A$ , воспользовавшись классическим определением вероятности. Общее число исходов испытания n = 30; число исходов испытания, благоприятствующих событию $A$ , равно m = 20; искомая вероятность $P(A)=\frac{m}{n}=\frac{20}{30}=\frac{2}{3}.$

2, а) Событие $B$ является независимым от события $A$ , так как появление или непоявление события $A$ не изменяет вероятности наступления события $B$ . Число исходов испытания, благоприятствующих событию $B$ , равно $m_{1}=20$ ; общее число исходов испытания $n=30$ ; следовательно, $P(B)=\frac{m_{1}}{n}=\frac{20}{30}=\frac{2}{3}.$
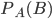2, б) Событие $B$ является зависимым от события $A$ , так как появление или непоявление события $A$ изменяет вероятность наступления события $B$ . Требуется найти вероятность события $B$ при условии, что и на кассете, взятой из кейса первой, записана музыка в стиле диско, то есть найти $P_{A}(B)$ - условную вероятность события $B$ , вычисленную при условии, что событие $A$ произошло. Так как кассета, взятая первой, назад в кейс не возвращается, то число исходов испытания, благоприятствующих событию $B$ , равно $m_{2}=19$ , а общее число исходов испытания равно $n_{1}=29$ . Искомая условная вероятность $P_{A}(B)=\frac{m_{2}}{n_{1}}=\frac{19}{29}.$
Задача №4. Используя исходные данные предыдущей задачи, найти вероятность того, что на двух наудачу взятых друг за другом кассетах записана музыка в стиле диско. Рассмотреть два случая: диджей, перед тем, как взять вторую кассету,
а) возвращает в кейс первую кассету;
б) не возвращает в кейс первую кассету.
Решение. Рассмотрим события:
А - на первой кассете записана музыка в стиле диско;
Б - на второй кассете записана музыка в стиле диско;
С - на двух взятых друг за другом кассетах записана музыка в стиле диско.
Событие С состоит в том, что и на первой, и на второй взятых из кейса кассетах записана музыка в стиле диско. Это означает, что событие С является произведением событий А и В: С=АВ.
Найдем вероятность события С, применив теорему умножения вероятностей.
а) A и В - независимые события. По формуле (13) получим