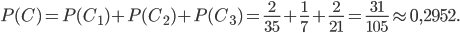Задача №1. Случайно смешаны кусты рассады двух сортов томатов: 9 кустов рассады сорта Белый налив и 7 - сорта Верлиока. Найти вероятность того, что первые три, посаженные друг за другом куста томатов, являются рассадой сорта Белый налив.
Решение. Испытание состоит в посадке одного куста рассады томата. Рассмотрим события:
 - куст, посаженный первым, - рассада томата сорта Белый налив;
- куст, посаженный первым, - рассада томата сорта Белый налив;
 - куст, посаженный вторым, - рассада томата сорта Белый налив;
- куст, посаженный вторым, - рассада томата сорта Белый налив;
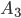 - куст, посаженный третьим, - рассада томата сорта Белый налив;
- куст, посаженный третьим, - рассада томата сорта Белый налив;
 - все три посаженные друг за другом куста являются рассадой томата сорта Белый налив.
- все три посаженные друг за другом куста являются рассадой томата сорта Белый налив.
Событие А состоит в том, что и первый, и второй, и третий кусты - рассада томата сорта Белый налив. Это означает, что событие А является произведением событий 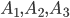 :
: 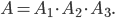
Найдем вероятность события А по теореме умножения вероятностей. События 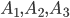 - зависимые, так как вероятность каждого последующего события (начиная со второго) изменяется в зависимости от того, произойдет или не произойдет предыдущее событие. По формуле (1) получим, что вероятность события
- зависимые, так как вероятность каждого последующего события (начиная со второго) изменяется в зависимости от того, произойдет или не произойдет предыдущее событие. По формуле (1) получим, что вероятность события  равна
равна 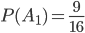 . Условная вероятность события
. Условная вероятность события  , вычисленная при условии, что событие
, вычисленная при условии, что событие  произошло, равна
произошло, равна 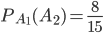 . Условная вероятность события
. Условная вероятность события 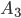 , вычисленная при условии, что произошли предыдущие два события, т. е. произошли и событие
, вычисленная при условии, что произошли предыдущие два события, т. е. произошли и событие  , и событие
, и событие  равна
равна 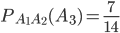 . В соответствии с формулой (14) при n=3 получим:
. В соответствии с формулой (14) при n=3 получим:
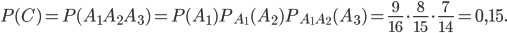
Задача №2. Слово МАШИНА составлено из букв разрезной азбуки. Наудачу друг за другом извлекают четыре буквы и выкладывают последовательно в ряд. Какова вероятность того, что получится слово ШИНА?
Решение. Испытание состоит в извлечении одной буквы. Рассмотрим события:
 - первoй извлечена буква Ш;
- первoй извлечена буква Ш; - второй извлечена буква И;
- второй извлечена буква И;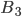 - третьей извлечена буква Н;
- третьей извлечена буква Н;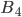 - четвертой извлечена буква А;
- четвертой извлечена буква А; - при произвольном извлечении четырех букв получится слово ШИНА.
- при произвольном извлечении четырех букв получится слово ШИНА.Событие
 состоит в том, что последовательно будут извлечены 4 нужные буквы: и буква Ш, и буква И, и буква Н, и буква А. Это означает, что событие
состоит в том, что последовательно будут извлечены 4 нужные буквы: и буква Ш, и буква И, и буква Н, и буква А. Это означает, что событие  является произведением событий
является произведением событий 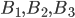 и
и 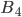 :
: 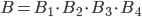 .
.Найдем вероятность события
 , применив теорему умножения вероятностей.
, применив теорему умножения вероятностей. 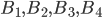 - зависимые события, так как наступление (или ненаступление) каждого предьщущего события изменяет вероятность наступления последующего. Найдем вероятность события
- зависимые события, так как наступление (или ненаступление) каждого предьщущего события изменяет вероятность наступления последующего. Найдем вероятность события  и условные вероятности событий
и условные вероятности событий 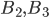 и
и 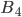 условиях, что наступят предыдущие им события. В данной задаче наступление предыдущих событий изменяет только общее число исходов испытаний для последующих событий. Число исходов испытаний, благоприятствующих событиям
условиях, что наступят предыдущие им события. В данной задаче наступление предыдущих событий изменяет только общее число исходов испытаний для последующих событий. Число исходов испытаний, благоприятствующих событиям 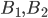 и
и 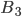 равно 1, так как в слове МАШИНА имеется по одной из нужных букв Ш, И и Н. Число исходов испытания, благоприятствующих событию
равно 1, так как в слове МАШИНА имеется по одной из нужных букв Ш, И и Н. Число исходов испытания, благоприятствующих событию 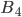 , равно 2, так как в слове МАШИНА имеются две буквы А, и в трех предыдущих испытаниях буква А не должна быть извлечена. Согласно формуле (14) получим
, равно 2, так как в слове МАШИНА имеются две буквы А, и в трех предыдущих испытаниях буква А не должна быть извлечена. Согласно формуле (14) получим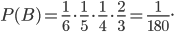
Задача №3. В урне 4 белых, б черных и 5 красных шаров. Из нее извлекают наугад один за другим два шара. Найти вероятность того, что оба шара одного цвета.
Решение. Рассмотрим события:
 - первым извлечен белый шар;
- первым извлечен белый шар;
 - вторым извлечен белый шар;
- вторым извлечен белый шар;
 - первым извлечен черный шар;
- первым извлечен черный шар;
 - вторым извлечен черный шар;
- вторым извлечен черный шар;
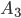 - первым извлечен красный шар;
- первым извлечен красный шар;
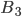 - вторым извлечен красный шар;
- вторым извлечен красный шар;
 - извлечены два шара одного цвета.
- извлечены два шара одного цвета.
Событие  представляет собой сумму следующих несовместных событий:
представляет собой сумму следующих несовместных событий:
 - извлечены два белых шара;
- извлечены два белых шара;
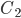 — извлечены два черных шара;
— извлечены два черных шара;
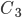 - извлечены два красных шара.
- извлечены два красных шара.
Таким образом, 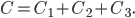
Событие  заключается в том, что и первый, и второй, извлеченные из урны шара, являются белыми. Это означает, что событие
заключается в том, что и первый, и второй, извлеченные из урны шара, являются белыми. Это означает, что событие  представляет собой произведение событий
представляет собой произведение событий  и
и  :
: 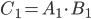 . Аналогично получим, что
. Аналогично получим, что 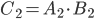 и
и 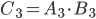 .
.
Вероятности событий  ,
, 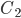 и
и 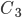 найдем по теореме умножения вероятностей.
найдем по теореме умножения вероятностей.
Событие  является зависимым от события
является зависимым от события  , так как его вероятность изменяется при наступлении события
, так как его вероятность изменяется при наступлении события  . Используя классическое определение вероятности, получим, что вероятность события
. Используя классическое определение вероятности, получим, что вероятность события  равна
равна 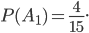 Условная вероятность события
Условная вероятность события  , вычисленная при условии, что событие
, вычисленная при условии, что событие  произошло, равна
произошло, равна 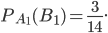 Согласно формуле (12) получим:
Согласно формуле (12) получим:
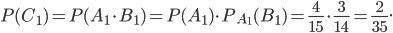
Рассуждая аналогично, найдем
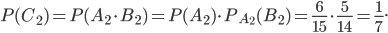
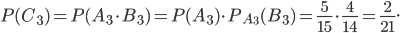
Вычислив
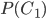 ,
, 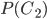 и
и 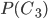 , найдем искомую вероятность
, найдем искомую вероятность 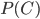 по теореме сложения вероятностей несовместных событий:
по теореме сложения вероятностей несовместных событий: