Касательная к плоской кривой (решение задач). Практикум по математическому анализу. Урок 37

Задача 1. В каких точках кривой $\displaystyle x=t-1,\: y=t^{3}-12t+1$ касательная параллельна: 1) оси $Ox$; 2) прямой $\displaystyle 9x+y+3=0$?
Решение. Используем здесь условие параллельности прямых, заключающееся в равенстве их угловых коэффициентов.
Найдем производную от $y$ по $x$ из уравнений кривой:
$\displaystyle y'=\frac{dy}{dt}:\frac{dx}{dt}=\frac{3t^{2}-12}{1}=3t^{2}-12.$
Эта производная представляет угловой коэффициент касательной к данной кривой в любой ее точке.
1) Приравнивая $y'$ угловому коэффициенту оси $Ox$, который равен нулю, получим $\displaystyle 3t^{2}-12=0;\: t^{2}=4;\: t=\pm 2$.
Подставляя эти значения параметра $t$ в данные уравнения кривой, найдем координаты тех ее точек, где касательная параллельна оси $Ox$: (1;— 15); (—3; 17).
2) Приравнивая $y'$ угловому коэффициенту данной прямой, который равен —9, получим $\displaystyle 3t^{2}-12=-9;\: t^{2}=1;\: t=\pm 1$.
По найденным значениям параметра $t$ из уравнений кривой определяем координаты искомых точек, где касательная к кривой параллельна данной прямой: (0; —10), (— 2; 12).
Задача 2. Составить уравнения касательных к параболе $\displaystyle y=x^{2}-4x+1$, проходящих через не лежащую на ней точку: 1) $O(0;0)$; 2) $A(1;1)$.
Решение. Уравнение касательной к данной параболе имеет общий вид

$$\displaystyle y-y_{0}=(x^{2}-4x+1)'_{0}(x-x_{0}),$$

или

$$\displaystyle y-(x_{0}^{2}-4x_{0}+1)=(2x_{0}-4)(x-x_{0}),$$

где $(x,y)$ — текущая точка на касательной; $\displaystyle (x_{0},y_{0})$ — неизвестная точка касания.
1) Так как касательная проходит через точку $O$, то
$\displaystyle 0-(x_{0}^{2}-4x_{0}+1)=(2x_{0}-4)(0-x_{0})$.
Решая это квадратное уравнение, находим для абсциссы точки касания $\displaystyle x_{0}$ два значения: $\displaystyle x_{0}=\pm 1$, а отсюда и уравнения двух касательных: $\displaystyle 2x+y=0$ и $\displaystyle 6x+y=0$.
2) Для точки $A$ те же рассуждения приводят к квадратному уравнению $\displaystyle x_{0}^{2}-2x_{0}+4=0$, корни которого комплексные. Поэтому через точку $A$ нельзя провести к данной параболе ни одной касательной.
Полученные результаты имеют простой геометрический смысл: из каждой точки, принадлежащей внешней области параболы, можно провести к ней две касательные, а из точки, принадлежащей ее внутренней области, — ни одной (рис. 1).

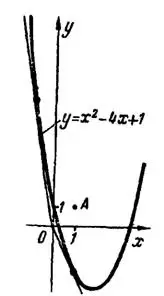
Рис.1

В общем случае задача о проведении касательных к кривой $y=f(x)$ через точку $(a,b)$, не лежащую на этой кривой, решается этим же способом, исходя из общего уравнения касательной

$$\displaystyle y-y_{0}=y'_{0}(x-x_{0}).$$

Эта задача имеет столько же решений, сколько вещественных корней имеет уравнение

$$\displaystyle b-f(x_{0})=f'(x_{0})(a-x_{0}).$$