1. Окружность.
Окружностью называется геометрическое место точек плоскости, равноудаленных от одной и той же точки этой плоскости (рис.1).
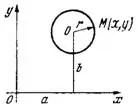
Уравнение окружности с центром в точке (а;b) и радиусом r имеет вид:
![]()
В частном случае, когда центр окружности лежит в начале координат, ее уравнением является
![]()
Общее уравнение кривой второго порядка
![]()
представляет окружность, если коэффициенты при квадратах координат равны между собой, А=С, и если отсутствует член с произведением координат ху, т.е. В=0.
2. Эллипс.
Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, равная 2а.
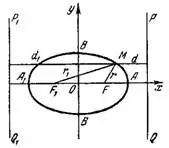
Каноническое уравнение эллипса имеет вид:
![]()
Координаты фокусов эллипса F(с;0) и F₁(-с;0). Расстояние между фокусами эллипса равно 2с. Точки пересечения эллипса с осями координат А(а;0), А₁(-а;0), B(0;b), B₁(0;-b) — называются вершинами.
Отрезки AA₁=2a, BB₁=2b называются осями эллипса. Эксцентриситет эллипса
![]()
Расстояния r и r₁ точки М(х;у) эллипса до его фокусов называются фокальными радиусами этой точки и определяются формулами
![]()
Две прямые PQ и P₁Q₁, параллельные малой оси эллипса и отстоящие от нее на расстоянии a/e называются директрисами эллипса. Их уравнения:
![]()
или
![]()
Отношение расстояний любой точки эллипса до фокуса и соответствующей директрисы есть величина постоянная, равная эксцентриситету эллипса:
![]()
Уравнение эллипса с осями, параллельными координатным осям, имеет вид
![]()
где (x₀,y₀) — координаты центра эллипса.







