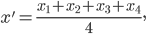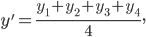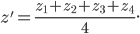1. Расстояние между двумя точками. Расстояние между двумя точками 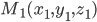 и
и 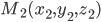 определяется по формуле:
определяется по формуле:
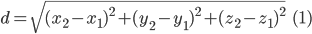
В частном случае, расстояние точки
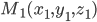 от начала координат равно:
от начала координат равно: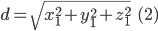
2. Деление отрезка в данном отношении. Если точка 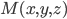 делит отрезок, определяемый точками
делит отрезок, определяемый точками 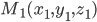 и
и 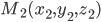 в отношении
в отношении 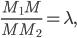 то ее координаты определяются по формулам:
то ее координаты определяются по формулам:
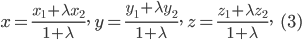
В частности, координаты середины отрезка
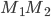 получаются при λ =1, т. е.
получаются при λ =1, т. е.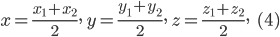
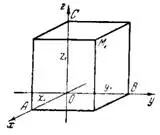
3. Определение направлений в пространстве. Пусть ось l образует с положительными направлениями осей координат Ох, Оу и Oz соответственно углы α, β и γ (рис.2). Числа
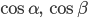 и
и  называются направляющими косинусами оси l.
называются направляющими косинусами оси l.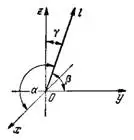
Между направляющими косинусами существует следующая основная зависимость:
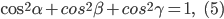
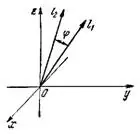
т. е. сумма квадратов направляющих косинусов любого направления равна единице.
Пусть 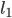 и
и 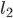 суть две оси, проходящие через начало координат (рис.3).
суть две оси, проходящие через начало координат (рис.3). 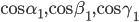 — направляющие косинусы
— направляющие косинусы 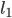 ,
, 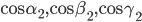 — направляющие косинусы
— направляющие косинусы 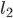 . Тогда косинус угла φ между этими осями вычисляется по формуле
. Тогда косинус угла φ между этими осями вычисляется по формуле
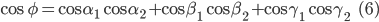
Пусть отрезок АВ (рис.4) задан своим началом
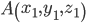 и концом
и концом 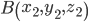 .
.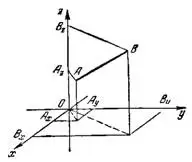
Тогда проекции этого отрезка на оси координат выражаются через координаты точек А и В следующими формулами:
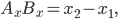
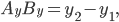
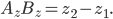
Длина отрезка АВ вычисляется по формуле:
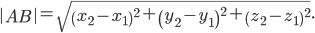
Тогда направляющие косинусы отрезка АВ равны:
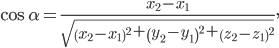
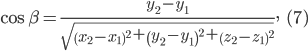
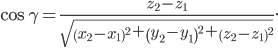
В частном случае, если начало отрезка находится в начале координат, а конец — в точке
 , то направляющие косинусы отрезка ОМ равны:
, то направляющие косинусы отрезка ОМ равны: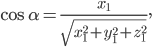
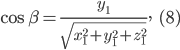
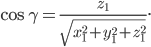
4. Нахождение центра тяжести пирамиды.
Пусть задана пирамида своими вершинами
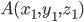 ,
, 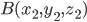 ,
, 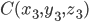 ,
, 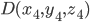 (рис.5).
(рис.5).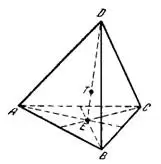
Центр тяжести пирамиды 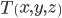 лежит на прямой, соединяющей любую из ее вершин с центром тяжести противолежащей грани. Находим координаты точки Е:
лежит на прямой, соединяющей любую из ее вершин с центром тяжести противолежащей грани. Находим координаты точки Е:
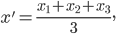
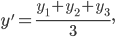
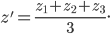
Искомая точка
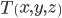 делит отрезок DE в отношении DT:TE = 3:1, т. е. λ =3.
делит отрезок DE в отношении DT:TE = 3:1, т. е. λ =3.Воспользуемся формулами (3) и получим: