Задача №1. Построить точки А (-3; 5; 1), В (1; -2; 4), С (2; 6; -1), D (4; 0; 3), Е (0; 7; 0), F (0; 0; 0). Объяснить расположение точек.
Построение. На оси Ох в отрицательном направлении откладываем 3 единицы выбранного масштаба. Из конца третьего отрезка проводим полупрямую вправо параллельно оси Оу и откладываем на ней 5 единиц выбранного масштаба (рис.1).
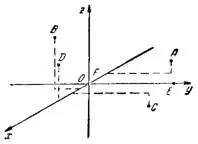
Из конца пятого отрезка проведем полупрямую вверх параллельно оси Оz и на ней отложим отрезок, равный 1. Конец этого отрезка и дает искомую точку А.
Аналогично строим остальные точки.
Точка А находится во втором октанте, точка В — в IV октанте, точка С — в V октанте; точка D лежит в плоскости xOz, точка Е лежит на оси Оу, а точка F в начале координат.
Задача №2. Дана точка А (3; 5; 2). Найти координаты точки, симметричной с точкой А:
а) относительно начала координат,
б) относительно плоскости xOz,
в) относительно оси Оу. Построить ее.
Решение. а) Точка А лежит в I октанте, симметричная ей точка относительно начала координат А₁ будет находиться в VII октанте. Ее координаты А₁(-3; -5; -2).
б) Точка А₂, симметричная точке А относительно плоскости xOz, будет находиться в IV октанте, следовательно, ее координаты А₂(3;-5; 2).
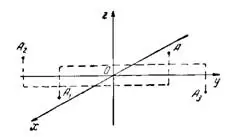
в) Точка А₃, симметричная точке А относительно оси Оу, будет находиться в VI октанте, следовательно, ее координаты А₃ (-3; 5; -2).
Решения этих задач подробно изложено в следующем видео
Задача №3. Показать, что один из внутренних углов треугольника А (3; 5; 3), В (2; -1; 4) и С (0; -2; 1) тупой.
Задача №4. На оси Oz найти точку, равноудаленную от двух точек А(-2; 1; 4) и В(3; 0; 1).
Решения этих задач подробно изложено в следующем видео
Задача №5. Определить координаты конца отрезка АВ, если известно, что его начало находится в точке А (-1; 2; 4) и точка С (2; 0; 2) отсекает от него третью часть.
Задача №6. Даны две вершины треугольника: А (- 3; -2; 2), В (4; 1; -2). Найти третью вершину С, зная, что сере¬дина стороны АС лежит на оси Оу, а середина стороны ВС — на плоскости xOz.
Решение. Обозначим середину стороны АС буквой М. Так как она лежит на оси Оу, то ее координаты М (0; у; 0). Середина стороны ВС, точка N, лежит на плоскости xOz, значит, ее координаты N (х₂; 0; z₂).
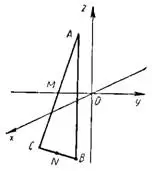
Воспользовавшись формулами деления отрезка пополам, найдем:


Следовательно,

Ответ: С (3; -1; -2).
Решения этих задач подробно изложено в следующем видео







