Примеры решения задач по теме "Метод координат в пространстве". Часть 2

Задача №1. Вычислить координаты точки М, если луч ОМ наклонен к оси Ох под углом в 60°, а к оси Оу — под углом в 45° и что длина его равна 12.
Решение. Согласно условию α =60°, β =45°.
Воспользовавшись соотношением между квадратами направляющих косинусов, найдем угол α:

$$\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma =1.$$

$$\frac{1}{4}+\frac{2}{4}+\cos ^{2}\gamma =1,\; \; \; \cos ^{2}\gamma =1-\frac{3}{4}=\frac{1}{4},$$

$$\cos \gamma =\pm \frac{1}{2};$$

$$\cos \gamma _{1}=\frac{1}{2},\; \; \gamma _{1}=60^{\circ};\; \; \; \cos \gamma _{2}=-\frac{1}{2},\; \; \gamma _{1}=120^{\circ}.$$

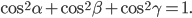
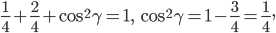
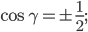
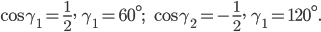
Координаты точки М определим по формулам:

$$x=d\cos \alpha ,\; \; y=d\cos \beta ,\; \; z=d\cos \gamma.$$

$$x=12\cos 60^{\circ}=12\cdot \frac{1}{2}=6; \; \; y=12\cos 45^{\circ}=12\cdot \frac{\sqrt{2}}{2}=6\sqrt{2}; \; \; z=12\cos \gamma=12\cdot \left ( \pm \frac{1}{2} \right )=\pm 6.$$

Задача №2. Начало отрезка находится в точке А (3; 2; 7). Найти его конец, зная, что длина отрезка АВ равна 15, а углы между этим отрезком и осями координат удовлетворяют соотношению
sin α : sin β : sin γ = 3 : 4 : 5.
Решения этих задач подробно изложено в следующем видео

Задача №3. Вершины треугольника находятся в точках А (5; 3; -10), В (0; 1; 4), С (-1; 3; 2). Найти направляющие косинусы биссектрисы угла В.
Задача №4. Найти угол между лучом, лежащим в плоскости yOz и образующим с осью Oz угол 60° и лучом, лежащим в плоскости xOz и образующим с осью Oz угол 30°.
Решения этих задач подробно изложено в следующем видео

Задача №5. Найти центр тяжести пирамиды, вершины которой находятся в точках: А (8; 10; 4), В (3; 4; 3), С(-2; 11; -5), D (1; -1; -4).
Решение. Центр тяжести пирамиды находим как среднее арифметическое координат вершин пирамиды.

$$x=\frac{8+3-2+1}{4}=\frac{10}{4}=\frac{5}{2}=2,5;\; \; \; y=\frac{10+4+11-1}{4}=\frac{24}{4}=6;$$

$$z=\frac{4+3-5-4}{4}=\frac{-2}{4}=-0,5.$$

Ответ: Т (2,5; 6; -0,5).
Задача №6. Найти отношение, в котором делится отрезок, соединяющий точки М (2; 2; 5) и N (2; —3; —5), центром тяжести пирамиды с вершинами в точках А (3; —2; 7), В (3; 3; 2), С (-7; 5; -3), D (9; -6; -2).
Решения этих задач подробно изложено в следующем видео