Величины, с которыми приходится встречаться в физике, механике и других прикладных дисциплинах, бывают двоякого рода: скалярные и векторные.
Скалярными величинами, или скалярами, называются величины, которые определяются только числовым значением.
Например: время, масса, плотность, длина отрезка, площадь, объем и т. д
Векторными величинами, или векторами, называются величины, которые определяются не только численным значением, но направлением и точкой приложения.
Например: сила, скорость, ускорение и т. д.
Векторные величины геометрически изображаются в виде отрезков, снабженных стрелками. Стрелка указывает направление, а длина отрезка изображает численные значения вектора и называется длиною, или модулем, или абсолютной величиной вектора.
![]()
Векторы обычно обозначаются либо буквой и черточкой над ней а, либо двумя буквами и черточкой над ними АВ, причем в этом случае первая буква указывает начало вектора, а вторая — его конец (рис.1).
Длина, или модуль, вектора 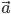 обозначается символом
обозначается символом  , либо символом
, либо символом  .
.
Два вектора называются равными, если они имеют одинаковые длины, лежат на параллельных прямых, либо на одной прямой, и направлены в одну сторону. Из определения равенства векторов следует, что при параллельном переносе вектора получается вектор, равный исходному. Поэтому начало вектора можно помещать в любой точке пространства. Выбрав некоторое начало — точку О, — удобно считать все векторы исходящими из этой точки. В таком случае мы будем говорить, что векторы приведены к общему началу О.
Если начало вектора совпадает с его концом, то вектор называется нулевым. Направление нулевого вектора неопределенно. Все нулевые векторы считаются равными друг другу.
Векторы, параллельные одной прямой, называются коллинеарными.
Векторы, параллельные одной плоскости, называются компланарными.







