Областью определения функции называется совокупность всех точек числовой оси, в которых она имеет определенные действительные значения.
Очевидно, для многих функций областью определения будет не вся числовая ось, а только некоторая ее часть. Так, для функции  областью определения является полуоткрытый интервал
областью определения является полуоткрытый интервал  ; для функции
; для функции  область определения состоит из двух интервалов:
область определения состоит из двух интервалов:  и
и  .
.
Основные элементарные функции имеют следующие области определения:
степенная функция  с рациональным положительным показателем
с рациональным положительным показателем  при нечетном
при нечетном  определена на всей числовой оси
определена на всей числовой оси  , а при четном
, а при четном  определена в интервале
определена в интервале  (при
(при  показатель
показатель  будет целым числом);
будет целым числом);
показательная функция определена на всей числовой оси;
логарифмическая функция определена в интервале  ;
;
тригонометрические функции  определены на всей числовой оси;
определены на всей числовой оси;  определены на всей числовой оси, исключая точки
определены на всей числовой оси, исключая точки  ;
;  определены на всей числовой оси, исключая точки
определены на всей числовой оси, исключая точки  ;
;
обратные тригонометрические функции  определены на отрезке
определены на отрезке  ;
;  определены на всей числовой оси.
определены на всей числовой оси.
При нахождении области определения элементарной функции, заданной формулой 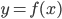 , нужно обращать внимание на следующие элементы формулы:
, нужно обращать внимание на следующие элементы формулы:
1) на радикалы четной степени — функция будет определена только для тех значений  при которых их подкоренные выражения будут неотрицательны;
при которых их подкоренные выражения будут неотрицательны;
2) на знаменатели дробных выражений — функция будет определена только для тех значений  , при которых знаменатели отличны от нуля;
, при которых знаменатели отличны от нуля;
3) на трансцендентные функции  , которые определены не всюду, а только при указанных выше значениях своего аргумента
, которые определены не всюду, а только при указанных выше значениях своего аргумента  .
.
Если эти перечисленные элементы отсутствуют в формуле 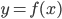 , то областью определения функции
, то областью определения функции  будет вся числовая ось (исключая те случаи, когда область определения функции ограничивается специальными условиями задачи).
будет вся числовая ось (исключая те случаи, когда область определения функции ограничивается специальными условиями задачи).
Область определения (существования) функции. Практикум по математическому анализу. Урок 4







