Пример 1. Найти область определения каждой из следующих функций:
1)  ; 2)
; 2) ![\displaystyle u=\frac{x-1}{x^{2}-5x+6}+\sqrt[3]{2x+1}](https://math-helper.ru/wp-content/plugins/latex/cache/tex_6918a4f726aec9c0253ef5cd498ec068.gif) ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  .
.
Решение.
1) Поскольку аргумент  содержится под радикалом четной степени, то функция
содержится под радикалом четной степени, то функция  будет иметь вещественные значения только при тех значениях
будет иметь вещественные значения только при тех значениях  , при которых подкоренное выражение будет неотрицательно, т.е.
, при которых подкоренное выражение будет неотрицательно, т.е.  . Решая это неравенство, получим
. Решая это неравенство, получим

Следовательно, область определения функции  есть отрезок [-1;1].
есть отрезок [-1;1].
2) Здесь аргумент  содержится в знаменателе дроби. Поэтому
содержится в знаменателе дроби. Поэтому  не может иметь тех значений, которые обращают знаменатель в нуль, так как деление на нуль не имеет смысла. Приравняв знаменатель нулю, найдем эти значения
не может иметь тех значений, которые обращают знаменатель в нуль, так как деление на нуль не имеет смысла. Приравняв знаменатель нулю, найдем эти значения  :
:

Второе слагаемое в выражении функции  не накладывает никаких ограничений на значения
не накладывает никаких ограничений на значения  , поскольку показатель радикала нечетный. Следовательно, областью определения функции
, поскольку показатель радикала нечетный. Следовательно, областью определения функции  является вся числовая ось, кроме точек
является вся числовая ось, кроме точек 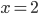 и
и 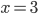 .
.
3) Функция  будет определена только для тех значений
будет определена только для тех значений  , для которых
, для которых  . Решив эти неравенства, получим
. Решив эти неравенства, получим

Отрезок [-1;2] и является областью определения функции  .
.
4) Найдем значения  , которые обращают знаменатель функции
, которые обращают знаменатель функции  в нуль:
в нуль:  .
.
При этих значениях  функция
функция  не имеет никаких значений.
не имеет никаких значений.
Областью определения функции  является вся числовая ось, кроме точек
является вся числовая ось, кроме точек  .
.
5) Логарифмическая функция 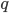 определена только для положительных значений своего аргумента (логарифмируемого выражения), поэтому .
определена только для положительных значений своего аргумента (логарифмируемого выражения), поэтому .
Решая это неравенство, получим , откуда следует, что  и
и  , т. е. область определения функции
, т. е. область определения функции 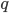 состоит из двух бесконечных интервалов
состоит из двух бесконечных интервалов  и
и  .
.
Область определения функции. Решение задач. Практикум по математическому анализу. Урок 5







