Построение графика функции по точкам. Практикум по математическому анализу. Урок 6

Наглядное графическое изображение функциональной зависимости между двумя переменными $x$ и $y$ можно получить, рассматривая значения этих переменных как координаты точек на плоскости.
Графиком функции, заданной уравнением $y=f(x)$, называется совокупность всех точек плоскости, координаты которых удовлетворяют этому уравнению.
Обычно график функции представляет некоторую плоскую линию.
Построение графика аналитически заданной функции по точкам выполняется в следующем порядке:
1) по данному аналитическому выражению функции составляется таблица соответствующих друг другу значений переменных;
2) выбирается система координат с подходящими единицами масштаба для каждой переменной.
Обычно применяется прямоугольная система координат и одна общая единица масштаба для обеих координатных осей;
3) строятся точки, координатами которых являются соответствующие друг другу значения аргумента и функции, содержащиеся в таблице;
4) полученные точки соединяются плавной линией.
Построенный этим способом график функции будет тем точнее, чем больше значений переменных содержится в таблице, чем больше точек будет нанесено на координатную плоскость.
Построение графика функции упрощается, если она является четной, нечетной или периодической. График четной функции симметричен относительно оси $Oy$; график нечетной функции симметричен относительно начала координату график периодической функции получается путем повторения части ее графика, соответствующей одному периоду.
Пример 1. Построить графики функций:
1) $\displaystyle y=x^{2}-2x-1$ на отрезке [—2; 4];
2) $\displaystyle y=-\frac{4x}{x^{2}+1}$ на отрезке [—5; 5];
3) $\displaystyle y=7x^{2}-100\sqrt{1+x^{2}}$ на отрезке $\displaystyle \left | x \right |\leq 7$;
4) $\displaystyle y=x^{2}-4\left | x-1 \right |+1$ на отрезке [-6; 5];
5) $\displaystyle y=\frac{16}{x^{2}}-1$ между точками пересечения с осью $Ox$.
Решение. 1) В условии задачи указано, что независимой переменной $x$ можно придавать только значения, заключенные на отрезке [—2; 4]. Учитывая это, составим следующую таблицу, беря для простоты только целые значения $x$ и вычисляя из данного уравнения соответствующие значения $y$:

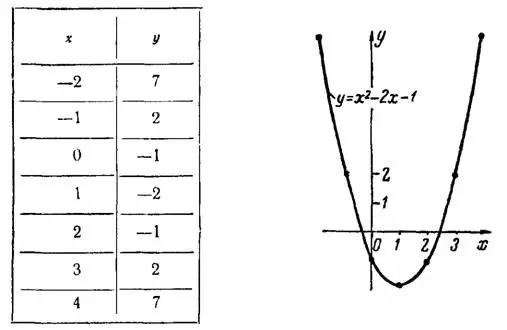
                                                                               Рис.1

Введем прямоугольную систему координат, как показано на рис. 1, с одинаковыми единицами масштаба, которые указаны числовыми пометками на координатных осях.
Построим точки, откладывая содержащиеся в таблице значения аргумента $x$ по оси абсцисс, а значения функции $y$ по оси ординат. Соединим полученные точки плавной кривой, которая и будет графиком данной функции. Эта кривая называется параболой.
Вообще графиком всякой квадратной функции $\displaystyle y=ax^{2}+bx+c$ является парабола, ось симметрии которой параллельна оси $Oy$.
2) Функция $\displaystyle y=-\frac{4x}{x^{2}+1}$ — нечетная, так как для нее $y(-x)=-y(x)$. Для значений аргумента, отличающихся только по знаку, значения нечетной функции будут также отличаться только по знаку. Поэтому при составлении таблицы здесь достаточно вычислить изданного уравнения значения функции только для положительных значений аргумента. Значения функции для отрицательных значений аргумента получим путем простои перемены знаков.

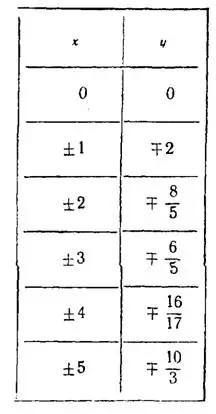
Выберем систему координат с одинаковыми масштабами на координатных осях (рис.2).
Построим точки для каждой пары числовых значений $x$ и $y$, которые содержатся в строках таблицы. Соединяя эти точки плавной кривой, получим график, симметричный относительно начала координат.

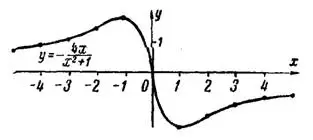
Рис.2

3) Функция $\displaystyle y=7x^{2}-100\sqrt{1+x^{2}}$ является четной, так как при перемене знака у любого значения аргумента значение этой функции не изменяется, $y(-x)=y(x)$. Поэтому здесь при составлении таблицы достаточно вычислить значения функции только для положительных значений аргумента; значения функции для отрицательных значений аргумента будут те же.

Составив таблицу, замечаем, что значения аргумента есть числа 1-го порядка, тогда как значения функции — числа 3-го порядка. Поэтому для построения соответствующих точек берем разные масштабы абсцисс и ординат; они показаны числовыми пометками на координатных осях (рис.3).

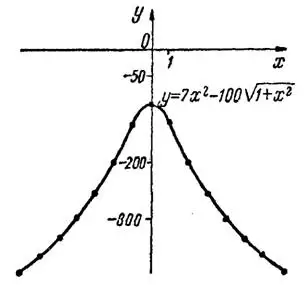
Рис.3

График данной четной функции симметричен относительно оси ординат.

4) Составим таблицу значений функции $\displaystyle y=x^{2}-4\left | x-1 \right |+1$ для значений аргумента $x$, заключенных на отрезке [—6; 5].
Затем строим точки и, соединяя их сплошной линией, получим искомый график (рис.4).
Данная функция не является четной или нечетной. Поэтому ее график не симметричен ни относительно оси $Oy$, ни относительно начала координат.

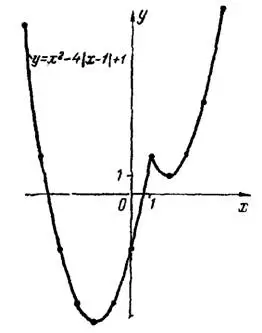
Рис.4

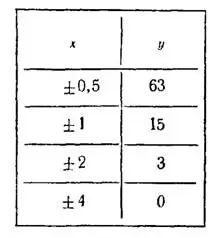
5) Абсциссы точек пересечения графика данной функции с осью $Ox$ найдем из данного уравнения, зная, что в этих точках ордината $y=0$. При $\displaystyle y=0,\; 16-x^{2}=0$, откуда $\displaystyle x=\pm 4$. Далее составляем таблицу значений данной четной функции на отрезке [—4; 4] и строим ее график (рис.5).

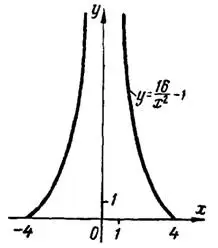
Рис.5

Когда $x$ приближается к нулю слева или справа, значения функции и ординаты ее графика неограниченно возрастают. При $x=0$ функция не имеет никакого числового значения, ее график состоит из двух отдельных бесконечных ветвей.