Задача №1. Составить простейшее уравнение гиперболы, если ее фокусы лежат на оси Оу и расстояние между ними равно 20; действительная ось гиперболы равна 16.
Решение. Уравнение гиперболы в этом случае будет иметь вид:
![]()
где b — действительная, а а — мнимая полуось гиперболы.
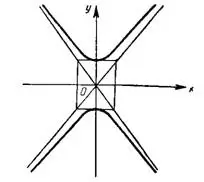
Согласно условию 2с = 20, с = 10; 2b =16, b = 8. Мнимую полуось а найдем из соотношения:
с² = а² + b²; а² = с² - b², а²= 100 — 64 = 36, а = 6.
Уравнение гиперболы будет:
![]()
Задача №2. Эксцентриситет гиперболы равен 1,5, фокальный радиус ее точки М, проведенный из некоторого фокуса, равен 12. Вычислить расстояние от точки М до односторонней с этим фокусом директрисы.
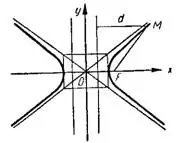
Решение. Если r — фокальный радиус точки М, а d — расстояние от точки М до односторонней с взятым
фокусом директрисы то ![]()
Откуда
![]()
Ответ: d = 8.
Решения этих задач подробно изложено в следующем видео
Задача №3. Прямые х=±4 служат директрисами гиперболы, эксцентриситет которой равен 1,5. Найти на гиперболе точки, фокальные радиусы которых, проведенные из правого фокуса, равны 9.
Решение этой задачи подробно изложено в следующем видео
Задача №4. Вычислить площадь треугольника, образован¬ного асимптотами гиперболы и прямой 4х - Зу - 8 = 0.
Задача №5. Составить уравнение гиперболы, зная, что рас¬стояние между ее вершинами равно 8 и фокусы ее находятся в точках (—3; 3) и (7; 3).
Решение этой задачи подробно изложено в следующем видео
Задача №6. Правый фокус гиперболы лежит в точке F (2; 2), и соответствующая директриса имеет уравнение х - 1/5 = 0.
Составить уравнение гиперболы, если точка A(11/3;6) лежит на гиперболе.
Решение этой задачи подробно изложено в следующем видео







