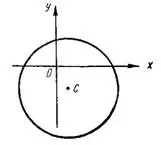
Задача №1. Определить центр и радиус окружности, заданной уравнением х²+у²-2х+4y-20=0.
Решение. Так как в заданном уравнении коэффициенты при х² и у² равны между собой и отсутствует член с произведением координат, го заданное уравнение действительно представляет собой уравнение окружности. Чтобы определить координаты центра и радиус окружности, необходимо уравнение привести к каноническому виду:
(х²-2х)+(y²+4у)=20, (x²-2х+1)+(у²+4х+4)=25, (x-1)²+(y+2)²=25.
Координаты центра и радиус окружности можно найти, не приводя данное уравнение к каноническому виду,
достаточно сравнить данное уравнение с уравнением окружности в общем виде:
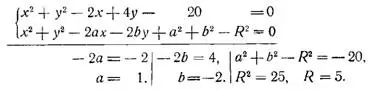
Ответ: (1, —2), R = 5.
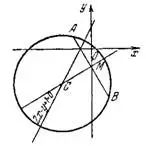
Задача №2. Составить уравнение окружности, проходя¬щей через точки А (—1;1) и В (1;-3), если центр ее лежит на прямой 2х-у+1=0.
Решение. Каноническое уравнение окружности:
Так как окружность проходит через точки А и B, то координаты этих точек должны удовлетворять уравнению окружности. Имеем два уравнения:
(-1-а)² + (1-b)²=r², (1-а)² + (-3-b)² = r².
Если центр окружности лежит на прямой 2х-у+1=0, то координаты центра также должны удовлетворить уравнению прямой.
Имеем третье уравнение: 2а-b+1=0.
Решим систему уравнений:
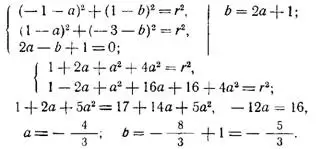
Таким образом, координаты центра окружности найдены:
![]()
Чтобы определить г², получим: г² = 1+2а+5а²,
![]()
Уравнение окружности:
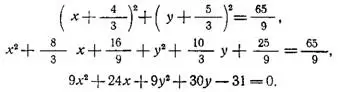
Ответ: 9х² + 9y² + 24x + 30у - 31 =0.
Задача №3. Составить уравнение окружности, если ее центр находится в точке С(5;4) и окружность отсекает от прямой х+2у-3=0 хорду, длина которой равна 8.
Решение. Искомое уравнение будет иметь вид:
(x-5)²+(у-4)²=r².
Определим расстояние центра С от данной прямой:
![]()
Так как радиус, перпендикулярный к хорде, делит ее пополам, то половина хорды будет равна 4 единицам.
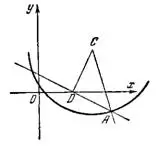
По теореме Пифагора имеем:
г²=4²+CD²=16+20=36, r² = 36, r = 6.
Уравнение окружности: (х -5)²+(у - 4)² = 36.
Ответ: (х -5)²+(у - 4)² = 36.
Задача №4. Составить уравнение окружности, касающейся двух параллельных прямых 2х+у-5=0 и 2х+y+15=0, причем одной из них — в точке А(2; 1).
Решение. Определим диаметр окружности, для чего используем формулу расстояния точки от прямой
![]()
Уравнение прямой 2x+y+15=0, точка А(2; 1)
![]()
Воспользовавшись координатами точки A, можем составить такое уравнение:
(2 - а)²+(1 - b)² = 20.
Второе уравнение с неизвестными а и b получим, определив расстояние точки С от первой прямой
![]()
Поскольку точка С лежит по одну сторону от прямой
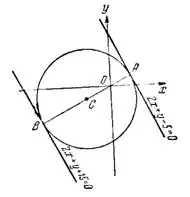
вместе с началом координат, то расстояние АС<0.
Имеем систему уравнений:
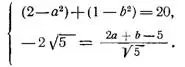
Решая полученную систему уравнений, найдем а=-2; b=-1.
Эту задачу рекомендуем решить самостоятельно другим способом.
Указания. Составить уравнение перпендикуляра А В к данным прямым и найти координаты точки В.
Ответ: (x+2)²+(у + 1)²=20.







