Решение задач на формулу Тейлора. Практикум по математическому анализу. Урок 46

Задача 2. Аппроксимировать функции: 1) $x^{m}$ и 2) $\ln x$ многочленами $n$- й степени относительно двучлена $x-1$ и оценить погрешность. Затем, полагая $x-1=t$, получить разложения функций по степеням $t$.
Решение. Чтобы аппроксимировать данную функцию $f(x)$ многочленом относительно двучлена $x-1$, следует написать для нее многочлен Тейлора, полагая $a=1$. Погрешность, возникающая при замене данной функции ее многочленом Тейлора, определяется величиной остаточного члена $R_{n}$ формулы Тейлора.
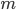1) Для функции $x^{m}$, где $m$ — любое вещественное число, имеем:
$f(x)=x^{m},\; \; \; \; f(1)=1,$
$f'(x)=mx^{m-1},\; \; \; f'(1)=m,$
$f''(x)=m(m-1)x^{m-2},\; \; \; f''(1)=m(m-1),$
$f'''(x)=m(m-1)(m-2)x^{m-3},\; \; \; f'''(1)=m(m-1)(m-2),$
..............................................
$f^{k}(x)=m(m-1)(m-2)...(m-k+1)x^{m-k},\; \; \; f^{k}(1)=m(m-1)(m-2)...(m-k+1).$
Пользуясь многочленом Тейлора (*), получим
$\displaystyle x^{m}\approx 1+\frac{m}{1!}(x-1)+\frac{m(m-1)}{2!}(x-1)^{2}+\frac{m(m-1)(m-2)}{3!}(x-1)^{3}+...+$
$\displaystyle +\frac{m(m-1)...(m-n+1)}{n!}(x-1)^{n}.$
Погрешность этого приближенного равенства найдем по общей формуле остаточного члена $R_{n}$ формулы Тейлора, полагая $\displaystyle f(x)=x^{m}$ и $a=1$:
$\displaystyle R_{n}=\frac{m(m-1)...(m-n)}{(n+1)!}(x-1)^{n+1}\left [ 1+\Theta (x-1) \right ]^{m-n-1},0<\Theta <1.$

Полагая $x-1=t$, получим
$\displaystyle (1+t)^{m}\approx 1+\frac{m}{1!}t+\frac{m(m-1)}{2!}t^{2}+\frac{m(m-1)(m-2)}{3!}t^{3}+...+\frac{m(m-1)...(m-n+1)}{n!}t^{n},\; (1)$
$\displaystyle R_{n}=\frac{m(m-1)...(m-n)}{(n+1)!}t^{n+1}(1+\Theta t)^{m-n-1}.$
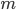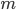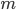Последняя формула представляет обобщение бинома Ньютона для любого показателя $m$. В частности, когда показатель $m$ — целое положительное число, то $R_{m}$ обращается в нуль, а равенство (1) обращается в элементарную формулу бинома Ньютона. Если $m$ не будет целым положительным числом, то равенство (1) дает приближенное выражение бинома в виде многочлена с биномиальными коэффициентами, которые составлены потому же закону, что и в элементарной формуле бинома Ньютона.
Как доказывается в теории рядов, погрешность $R_{n}$ биномиальной формулы (1) может быть сделана сколь угодно малой величиной, т. е. стремится к нулю с возрастанием $n$ только для тех значений $t$, которые по абсолютному значению меньше единицы:

$$-1<t<1.$$

Полагая $n=1,2,3$, получим простейшие приближенные биномиальные формулы: $(1+t)^{m}\approx 1+mt,$ $\displaystyle (1+t)^{m}\approx 1+mt+\frac{m(m-1)}{2}t^{2},$ $\displaystyle (1+t)^{m}\approx 1+mt+\frac{m(m-1)}{2}t^{2}+\frac{m(m-1)(m-2)}{6}t^{3}.$
Вторая из этих формул точнее первой, а третья точнее второй.
2) Для функции $\ln x$ получим:
$f(x)=\ln x,\; \; \; \; f(1)=0,$
$f'(x)=x^{-1},\; \; \; \; f'(1)=1,$
$f''(x)=-1\cdot x^{-2},\; \; \; \; f''(1)=-1,$
$f'''(x)=1\cdot2\cdot x^{-3},\; \; \; \; f'''(1)=2!,$
$f^{(4)}(x)=-1\cdot2\cdot 3\cdot x^{-4},\; \; \; \; f^{(4)}(1)=-3!,$
................................................
$\displaystyle f^{(k)}(x)=(-1)^{k-1}(k-1)!\ x^{-k}, f^{(k)}(1)=(-1)^{k-1}\cdot (k-1)!$
$\displaystyle \ln x\approx \frac{x-1}{1}-\frac{(x-1)^{2}}{2}+\frac{(x-1)^{3}}{3}-...+(-1)^{n-1}\frac{(x-1)^{n}}{n}.$
Погрешность этой приближенной формулы
$\displaystyle R_{n}=\frac{(-1)^{n}}{n+1}\left [ \frac{x-1}{1+\Theta (x-1)} \right ]^{n+1},\: 0<\Theta <1.$
Полагая $x-1=t$, получим
$\displaystyle \ln (1+t)\approx t-\frac{t^{2}}{2}+\frac{t^{3}}{3}-\frac{t^{4}}{4}+...+(-1)^{n-1}\frac{t^{n}}{n};\; \;\;\;(2)$
$\displaystyle R_{n}=\frac{(-1)^{n}}{n+1}\left [ \frac{t}{1+\Theta t} \right ]^{n+1}.$
Здесь $\displaystyle R_{n} \to 0$ с возрастанием $n$ при $-1<t\leq 1$, т. е. погрешность вычисления логарифмов по формуле (2) можно довести до любой сколь угодно малой величины только для значений $t$ из указанного полуоткрытого интервала. При $n=1,2,3$ получим приближенные формулы
$\ln (1+t)\approx t,$
$\displaystyle \ln (1+t)\approx t-\frac{t^{2}}{2},$
$\displaystyle \ln (1+t)\approx t-\frac{t^{2}}{2}+\frac{t^{3}}{3},$
которые следуют в порядке возрастающей точности.
Аналогичным образом, многие другие трансцендентные и сложные алгебраические функции можно аппроксимировать посредством формулы Тейлора простейшими алгебраическими функциями — степенными многочленами с любой
заданной точностью, что имеет огромное теоретическое и практическое значение.