Схема применения определенного интеграла к вычислению различных величин. Урок 83

Схема применения определенного интеграла к вычислению различных величин. Площадь плоской фигуры. Практикум по математическому анализу. Урок 83
Понятие определенного интеграла вследствие его абстрактности широко применяется для вычисления различных геометрических и физических величин.
Для вычисления некоторой величины и при помощи определенного интеграла можно руководствоваться следующей общей схемой (I):
1. Разбить $u$ на большое число $n$ малых слагаемых элементов $\Delta u_{i}$:

$$\displaystyle u=\Delta u_{1}+\Delta u_{2}+...+\Delta u_{n}=\sum_{i=1}^{n}\Delta u_{i}.$$

2. Найти приближенное значение каждого элемента $\Delta u_{i}$ в виде произведения $\Delta u_{i}\approx f(x_{i})\cdot \Delta x$ и затем приближенное значение $u$ в виде интегральной суммы

$$\displaystyle u\approx \sum_{i=1}^{n}f(x_{i})\Delta x,\; \; \; \; \; (*)$$

где $x$ — один из параметров величины который по условию задачи изменяется в известном интервале $\displaystyle a\leq x\leq b$; $f(x)$ - данная или определяемая из условия задачи функция от $x$; $x_{0}=a,x_{1},x_{2},...,x_{n}=b$ — точки интервала $\left [ a;b \right ]$, которые при разбиении $u$ на $n$ элементов разбивают этот интервал на $n$ равных частей $\Delta x=\frac{b-a}{n}$.
Здесь при нахождении приближенного значения малого элемента $\Delta u_{i}$ используются различные допущения. Например, здесь допустимо малые криволинейные отрезки заменять стягивающими их хордами; переменную силу (или скорость) на малых участках пути здесь можно заменять постоянной силой (или скоростью),— допуская, что она неизменно сохраняет на всем малом участке пути ту величину и то направление, которые она имела в начальной или конечной точке этого малого участка; переменную температуру непрерывно нагреваемого или охлаждаемого тела в течение малых промежутков времени здесь можно считать постоянной, допуская, что в течение каждого малого промежутка времени она неизменно сохраняет то значение, которое имела в начале или в конце этого промежутка.
3. Если из условия задачи следует, что при $n\rightarrow + \infty$ погрешность приближенного равенства (*) стремится к нулю, то искомая величина $u$ будет численно равна определенному интегралу $\displaystyle u=\int_{a}^{b}f(x)dx$.
Многие величины можно выразить посредством определенного интеграла, пользуясь другой схемой (II):
1. Полагаем, что некоторая часть искомой величины $U$ есть неизвестная функция $u(x)$, где $x$ — один из параметров величины $U$, который изменяется в известном из условия задачи интервале $\displaystyle a\leq x\leq b$.
2. Найдем дифференциал $du$ функции $u(x)$, т. е. приближенную величину (главную часть) ее приращения $\Delta u$ при изменении $x$ на малую величину $\Delta x$ в виде произведения $du=f(x)dx$, где $f(x)$ данная или определяемая из условия задачи функция от $x$.
При этом здесь также используются различные допущения, которые в общем сводятся к тому, что при изменении аргумента $x$ на малую величину $dx$ изменение функции $u(x)$ считается пропорциональным $dx$.
3. Убедившись, что дифференциал $du$ найден верно, что при $dx\rightarrow 0$ бесконечно малые $\Delta u$ и $du$ будут эквивалентны, найдем искомую величину $U$, интегрируя $du$ в пределах от $x=a$ до $x=b$:

$$\displaystyle U=\int_{a}^{b}f(x)dx.$$

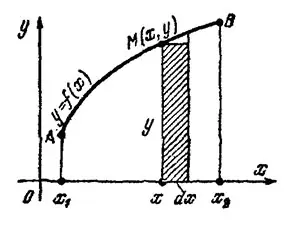
Рис. 1

Так, согласно схеме II:
а) Для криволинейной трапеции, прилежащей к оси $Ox$, рис.1, дифференциал переменной площади $\displaystyle S(x)=S_{x_{1}AMx}$ есть площадь прямоугольника со сторонами $y$ и $dx$, т. е. $dS=ydx$.
Площадь $\displaystyle S(x)=S_{x_{1}ABx_{2}}$ если вся трапеция расположена над осью $Ox$ выражается интегралом

$$\displaystyle S=\int_{x_{1}}^{x_{2}}ydx.\; \; \; \; \; \; \; \; (1)$$

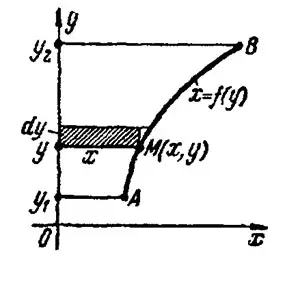
Рис. 2

б) Для криволинейной трапеции, прилежащей к оси $Oy$, рис.2, дифференциал переменной площади $\displaystyle S(y)=S_{y_{1}AMy}$ есть площадь прямоугольника со сторонами $x$ и $dy$, т. е. $dS=xdy$.
Площадь $\displaystyle S(y)=S_{y_{1}ABy_{2}}$, если вся трапеция расположена справа от оси $Oy$, выражается интегралом

$$\displaystyle S=\int_{y_{1}}^{y_{2}}xdy.\; \; \; \; \; \; \; (2)$$

В частности каждая из параллельных сторон трапеции может свестись к точке.
Площадь всякой плоской фигуры, отнесенной к прямоугольной системе координат, может быть составлена из площадей криволинейных трапеций, прилежащих к оси Ох или к оси Оу.

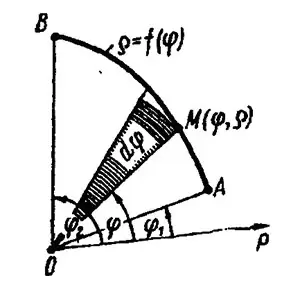
Рис. 3

в) Дифференциал переменной площади $S(\varphi )=S_{OAM}$, рис.3, есть площадь кругового сектора с центральным углом $d\varphi$ и радиусом $\rho$, т. е.

$$\displaystyle dS=\frac{1}{2}\rho ^{2}d\varphi.$$

Площадь криволинейного сектора $OAB$ выражается формулой

$$\displaystyle S=\frac{1}{2}\int_{\varphi _{1}}^{\varphi _{2}}\rho ^{2}d\varphi.\; \; \; \; \; \; \; \; \; (3)$$

В частности точка $A$ или $B$ или обе они могут совпасть с полюсом $O$.
Площадь всякой плоской фигуры, отнесенной к полярной системе координат, может быть составлена из площадей криволинейных секторов.