Пример 1. Вычислить площадь, ограниченную следующими линиями:
1) параболой 
и прямой 
;
2) параболами 
и 
;
3) кубическими параболами 
и 
;
4) эллипсом 
;
5) кардиоидой 
;
6) окружностями 
и 
.
Решение. 1) Совместно решая данные уравнения, определим две точки пересечения линий, ограничивающих искомую площадь, 
.
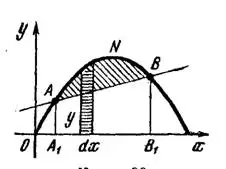
Рис. 90
Построив эти точки и проходящие через них данные линии, рис. 90, видим, что искомая площадь 
равна разности площадей 
и 
. Площадь 
согласно формуле
выражается интегралом
Площадь
трапеции 
равна произведению полусуммы ее оснований на высоту:
Следовательно, искомая площадь
Если за единицу длины принят дециметр, то
кв. дм.
Рис. 91
2) Определив точки пересечения парабол 
и 
и построив эти точки и параболы, рис. 91, видим, что искомую площадь 
можно найти как алгебраическую сумму площадей криволинейных трапеций: 
.
Площадь
расположена под осью 
, поэтому, чтобы получить ее величину с положительным знаком, пределы интегрирования взяты справа налево.
Следовательно,
Площадь можно найти иначе, определив ее дифференциал 
как площадь прямоугольника, у которого высота есть разность ординат данных парабол, а основание 
, рис. 91:
Отсюда
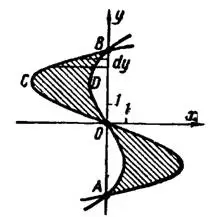
Рис. 92
3) Находим три точки пересечения данных парабол: 
, затем строим эти точки и параболы, рис. 92.
Искомая площадь состоит из двух одинаковых частей; половину ее можно найти как разность площадей криволинейных трапеций 
и 
, прилежащих к оси 
. Согласно формуле
имеем
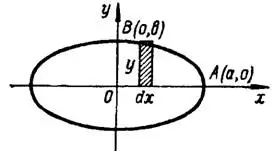
Рис. 93
4) Оси координат совпадают с осями симметрии данного эллипса (рис. 93), и поэтому они делят его на четыре одинаковые части. Четвертую часть искомой площади , расположенную в первом квадранте, найдем как площадь криволинейной трапеции, прилежащей к оси :
Пользуясь данными параметрическими уравнениями эллипса, преобразуем интеграл к переменной
: 
когда 
, то 
когда 
, то 
;
Отсюда при
получается формула для площади круга: 
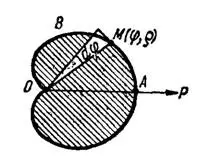
Рис. 94
5) Кардиоида симметрична относительно полярной оси (рис. 94). Поэтому искомая площадь равна удвоенной площади
криволинейного сектора 
. Дуга 
описывается концом полярного радиуса 
при изменении полярного угла 
от 0 до 
. Поэтому согласно формуле
![S=2\cdot \frac{1}{2}\int_{0}^{\pi }\rho ^{2}d\varphi =a^{2}\int_{0}^{\pi}(1+\cos \varphi)^{2}d\varphi =a^{2}\int_{0}^{\pi}(1+2\cos \varphi +\cos ^{2}\varphi )d\varphi =a^{2}\left [ \int d\varphi +2\int \cos \varphi d\varphi +\frac{1}{2}\int (1+\cos 2\varphi )d\varphi \right ]\left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{\pi}=\frac{3}{2}\pi a^{2}.](https://math-helper.ru/wp-content/plugins/latex/cache/tex_65382713432adf49a0266ac38a08c5c7.gif)
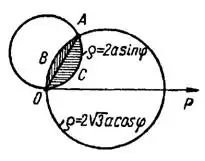
Рис. 95
6) Решив совместно данные уравнения, найдем точку пересечения окружностей 
. Построив окружности, рис. 95, видим, что искомая площадь равна сумме площадей криволинейных секторов 
и 
.
Дуга описывается концом полярного радиуса большей окружности при изменении полярного угла 
от 
до 
, поэтому
Дуга
описывается концом полярного радиуса меньшей окружности при изменении полярного угла от 0 до , поэтому
Следовательно,
