Если известна площадь  любого сечения тела плоскостью, параллельной некоторой плоскости
любого сечения тела плоскостью, параллельной некоторой плоскости 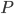 , где
, где  —расстояние сечения от плоскости
—расстояние сечения от плоскости 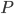 , рис.1, то при изменении
, рис.1, то при изменении  на величину
на величину  дифференциал объема тела равен объему прямого цилиндра с высотой
дифференциал объема тела равен объему прямого цилиндра с высотой  и площадью основания
и площадью основания  , т. е.
, т. е.  , а объем всего тела выражается интегралом
, а объем всего тела выражается интегралом

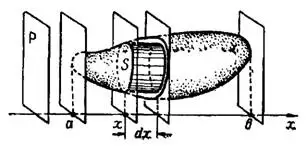
Рис. 1
где  и
и  — левая и правая границы изменения
— левая и правая границы изменения  .
.
Задача 1. Найти объем части цилиндра, отсеченной плоскостью, которая проходит через диаметр  его основания под углом
его основания под углом  к плоскости основания.
к плоскости основания.
Решение. Изобразив половину данного тела, рис. 2, замечаем, что всякое сечение его плоскостью, параллельной плоскости  , представляет прямоугольный треугольник.
, представляет прямоугольный треугольник.
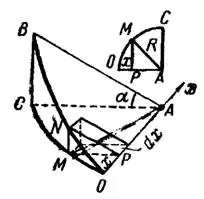
Рис. 2
Найдем площадь сечения, отстоящего от точки  на расстоянии
на расстоянии  . Из прямоугольного треугольника
. Из прямоугольного треугольника  имеем
имеем  . Из прямоугольного треугольника
. Из прямоугольного треугольника  имеем
имеем  .
.
Площадь сечения  , как прямоугольного треугольника с катетами
, как прямоугольного треугольника с катетами 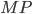 и
и 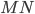 :
:
![\displaystyle S(x)=\frac{1}{2}MP\cdot MN=\frac{1}{2}MP^{2}\, \textrm{tg}\, \alpha=\frac{1}{2}\left [ R^{2}-(R-x)^{2} \right ]\, \textrm{tg}\, \alpha=\frac{1}{2}(2Rx-x^{2})\, \textrm{tg}\, \alpha.](https://math-helper.ru/wp-content/plugins/latex/cache/tex_6bab05a3fb05e3928f4e61b0241d166a.gif)
При изменении
 на величину
на величину  объем
объем  изменится на величину
изменится на величину  эквивалентную объему прямого цилиндра (призмы) с высотой
эквивалентную объему прямого цилиндра (призмы) с высотой  и площадью основания
и площадью основания  :
:
Всему искомому объему соответствует изменение
 от 0 до
от 0 до  , поэтому
, поэтому
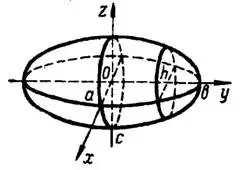
Рис. 3
Задача 2. Найти объем трехосного эллипсоида

Решение. Плоское сечение эллипсоида, параллельное плоскости
 и отстоящее от нее на расстоянии
и отстоящее от нее на расстоянии  , рис. 3, представляет эллипс
, рис. 3, представляет эллипс
с полуосями

Площадь этого сечения, как площадь эллипса, найдем по формуле, полученной в решении задачи 1(4) (урок 84),

Подставляя в формулу (*), получим объем всего эллипсоида

При
 полученная формула для объема эллипсоида преобразуется в формулу для объема шара
полученная формула для объема эллипсоида преобразуется в формулу для объема шара  .
.Задача 3. Найти объем, общий двум цилиндрам:  (ограниченный данными цилиндрическими поверхностями).
(ограниченный данными цилиндрическими поверхностями).
Решение. Построим восьмую часть тела, расположенную в первом октанте, рис. 4.
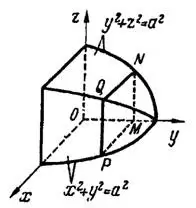
Рис. 4
Любое сечение тела плоскостью, параллельной плоскости  , представляет квадрат. Площадь сечения
, представляет квадрат. Площадь сечения  , отстоящего от плоскости
, отстоящего от плоскости  на расстоянии
на расстоянии  , найдем как площадь квадрата со стороной
, найдем как площадь квадрата со стороной

Весь искомый объем, согласно формуле (*), выразится интегралом








