Объем тела вращения. Практикум по математическому анализу. Урок 86

Если тело образуется при вращении вокруг оси $Ox$ криволинейной трапеции $\displaystyle x_{1}ABx_{2}$ (рис. 1), то любое его плоское сечение, перпендикулярное коси $Ox$, будет круг, радиус которого равен соответствующей ординате кривой $y=f(x)$.

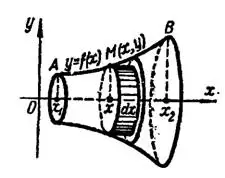
Рис. 1

Площадь сечения $S(x)$, соответствующего абсциссе $x$, как площадь круга, равна $\pi y^{2}$.
Дифференциал объема тела, соответствующий приращению $dx$, будет $\displaystyle dv=\pi y^{2}dx$, а весь объем тела вращения определяется формулой

$$\displaystyle V=\pi \int_{x_{1}}^{x_{2}}y^{2}dx\; (x_{1}<x_{2})\; \; \; \; \; (A)$$

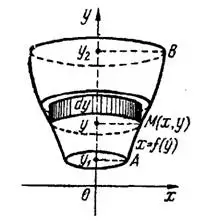
Рис. 2

Если тело образуется при вращении вокруг оси $Oy$ криволинейной трапеции $\displaystyle y_{1}ABy_{2}$, прилежащей к оси $Oy$, рис. 2, то $\displaystyle dv=\pi x^{2}dy$,

$$\displaystyle V=\pi \int_{y_{1}}^{y_{2}}x^{2}dy\; (y_{1}<y_{2})\; \; \; \; \; (B)$$

Задача 1. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями:
1) $\displaystyle y^{2}=2px,\: x=a$ вокруг оси $Ox$;
2) $\displaystyle \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ вокруг оси $Oy$;
3) $\displaystyle 2y=x^{2}\: 2x+2y-3=0$ вокруг оси $Ox$;
4) $\displaystyle x=a\, \cos ^{3}t,\: y=a\, \sin ^{3}t$ вокруг оси $Ox$;
5) $\displaystyle y=4-x^{2},\: y=0$ вокруг прямой $x=3$.

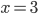Решение. 1) Построив параболу $\displaystyle y^{2}=2px$ и прямую $x=a$ получим параболический сегмент $OAB$, рис. 3. При вращении его вокруг оси Ох образуется сегмент параболоида вращения. Объем этого тела, согласно общим указаниям, найдем по формуле (А):

$$\displaystyle V=\pi \int_{x_{1}}^{x_{2}}y^{2}dx=\pi \int_{0}^{a}2pxdx=\pi px^{2}\left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{a}=\pi pa^{2}.$$

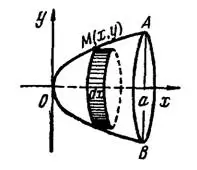
Рис. 3

2) Если у данного эллипса $b<a$, то при вращении его вокруг малой оси получается сжатый эллипсоид вращения, рис. 4. Вычислим объем $\displaystyle V_{1}$ этого тела по формуле (В):

$$\displaystyle V_{1}=\pi \int_{y_{1}}^{y_{2}}x^{2}dy=\pi a^{2}\int_{-b}^{b}\left ( y-\frac{y^{2}}{b^{2}} \right )dy=2\pi a^{2}\left ( y-\frac{y^{3}}{3b^{2}} \right )\left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{b}=\frac{4}{3}\pi a^{2}b.$$

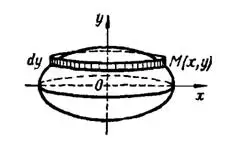
Рис. 4

При вращении эллипса вокруг его большой оси получается удлиненный эллипсоид вращения, рис. 5, объем которого
$\displaystyle V_{2}=\frac{4}{3}\pi ab^{2}$. Очевидно,

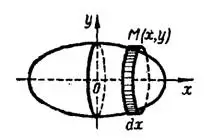
Рис. 5

3) Ограниченная данными линиями фигура $OAB$, рис. 6, при вращении вокруг оси $Ox$ образует тело, объем которого можно найти как разность объемов тел, образованных вращением вокруг оси $Ox$ трапеций $\displaystyle A_{1}ABB_{1}$ и $\displaystyle A_{1}AOBB_{1}$.
Объем $\displaystyle V_{1}$, образованный вращением трапеции $\displaystyle A_{1}ABB_{1}$, можно найти по формуле (А):

$$\displaystyle V_{1}=\pi \int_{x_{1}}^{x_{2}}y^{2}dx=\pi \int_{-3}^{1}(1,5-x)^{2}dx=\pi \int_{-3}^{1}(1,5-x)^{2}d(1,5-x)=\frac{\pi (1,5-x)^{3}}{3}\left.\begin{matrix} \\ \\ \end{matrix}\right| _{-3}^{1}=\frac{91}{3}\pi$$

или как объем усеченного конуса по формуле элементарной геометрии.

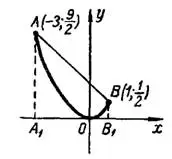
Рис. 6

Объем 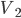$\displaystyle V_{2}$, образованный вращением криволинейной трапеции $\displaystyle A_{1}AOBB_{1}$, найдем по формуле (А):

$$\displaystyle V_{2}=\frac{\pi }{4}\int_{-3}^{1}x^{4}dx=\frac{\pi }{4}\cdot \frac{x^{5}}{5}\left.\begin{matrix} \\ \\ \end{matrix}\right| _{-3}^{1}=\frac{\pi }{20}(1+243)=\frac{61}{5}\pi .$$

Искомый объем $\displaystyle V=V_{1}-V_{2}=18\frac{2}{15}\pi.$

4) Фигура, ограниченная астроидой, рис. 7, при вращении вокруг оси $Ox$ образует тело вращения, объем которого определяется формулой (А):

$$\displaystyle V=\pi \int_{x_{1}}^{x_{2}}y^{2}dx=\pi \int_{-a}^{a}y^{2}dx=2\pi \int_{0}^{a}y^{2}dx.$$

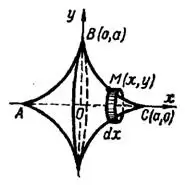
Рис. 7

Исходя из данных параметрических уравнений астроиды $\displaystyle x=a\, \cos ^{3}t,\: y=a\, \sin ^{3}t$, преобразуем последний интеграл к переменной $t$: $\displaystyle y^{2}=a^{2}\, \sin ^{6}t;\: dx=-3a\, \cos ^{2}t\sin tdt;\: t=\frac{\pi }{2}$ при $x=0$;
$t=0$ при $x=a$;

$$\displaystyle V=2\pi \int_{0}^{a}y^{2}dx=-6a^{3}\pi \int_{\frac{\pi }{2}}^{0}\sin ^{6}t\cos ^{2}t\sin tdt.$$

Далее тождественно преобразуем подынтегральное выражение и, применяя формулу интегрирования степени, получим

$$\displaystyle V=6a^{3}\pi \int_{\frac{\pi }{2}}^{0}(1-\cos ^{2}t)^{3}\cos ^{2}t(-\sin t)dt=6a^{3}\pi \int_{\frac{\pi }{2}}^{0}(\cos ^{2}t-3\cos ^{4}t+3\cos ^{6}t-\cos ^{8}t)d\cos t=6a^{3}\pi\left ( \frac{1}{3}\cos ^{3}t-\frac{3}{5}\cos ^{5}t+\frac{3}{7}\cos ^{7}t-\frac{1}{9}\cos ^{9}t \right )\left.\begin{matrix} \\ \\ \end{matrix}\right| _{\frac{\pi }{2}}^{0}=\frac{32}{105}\pi a^{3}.$$

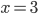5) Параболический сегмент $ABC$, ограниченный параболой $\displaystyle y=4-x^{2}$ и осью $Ox$, рис. 8, при вращении вокруг прямой $x=3$ образует тело, любое сечение которого плоскостью, перпендикулярной к оси вращения, представляет круговое кольцо, ограниченное концентрическими окружностями. Площадь такого сечения, отстоящего от начала координат на расстоянии $y$,

$$\displaystyle S=\pi R^{2}-\pi r^{2}=\pi \left | (3+x)^{2}-(3-x)^{2} \right |=12\pi x=12\pi \sqrt{4-y},$$

так как $x$ есть абсцисса точки, лежащей на данной параболе, т. е. $\displaystyle x=\sqrt{4-y}$.
При изменении $y$ на величину $dy$ дифференциал объема тела будет $\displaystyle dv=S(y)dy=12\pi \sqrt{4-y}\, dy.$

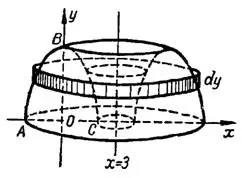
Рис. 8

Весь искомый объем получается при изменении $y$ от 0 до 4. Поэтому, интегрируя $dv$ в этих пределах, получим

$$\displaystyle V=12\pi \int_{0}^{4}\sqrt{4-y}\, dy=-12\pi \int_{0}^{4}(4-y)^{\frac{1}{2}}d(4-y)=8\pi (4-y)^{\frac{3}{2}}\left.\begin{matrix} \\ \\ \end{matrix}\right| _{4}^{0}=64\pi .$$