Длина дуги плоской кривой. Практикум по математическому анализу. Урок 87

Если плоская кривая отнесена к прямоугольной системе координат и задана уравнением $y=f(x)$, или $x=F(y)$ или параметрическими уравнениями $x=\varphi (t),\: y=\psi (t)$, то дифференциал $dl$ длины ее дуги, рис. 1, выражается формулой

$$dl=\sqrt{1+(y')^{2}}dx=\sqrt{1+(x')^{2}}dy=\sqrt{x^{2}+y^{2}}dt,$$

а длина дуги $AB$ определяется формулой

$$\displaystyle L_{AB}=\int_{(A)}^{(B)}dl=\int_{x_{A}}^{x_{B}}\sqrt{1+(y')^{2}}dx=\int_{y_{A}}^{y_{B}}\sqrt{1+(x')^{2}}dy=\int_{t_{A}}^{t_{B}}\sqrt{x^{2}+y^{2}}dt.\; \; \; \; \; (1)$$

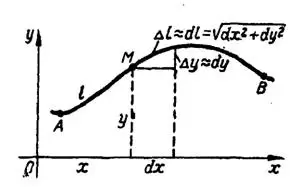
Рис. 1

Если плоская кривая отнесена к полярной системе координат и задана уравнением $\rho =f(\varphi )$ (рис. 2), то

$$\displaystyle dl=\sqrt{\rho ^{2}+(\rho ')^{2}}d\varphi.\; \; \; \; \; \; (2)$$

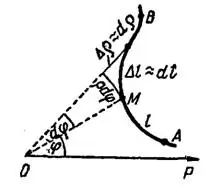
Рис. 2

Пример 1. Вычислить длину дуги:
1) полукубической параболы $\displaystyle y^{2}=(x-1)^{3}$ между точками $A(2;-1)$ и $B(5;-8)$;
2) одной арки циклоиды $x=a(t-\sin t),\: y=a(1-\cos t)$;
3) кривой $\displaystyle \rho =a\cos ^{3}\frac{\varphi }{3}$.
Решение.
1) Разрешаем данное уравнение относительно $y$ и находим $y'$:

$$\displaystyle y=\pm (x-1)^{\frac{3}{2}};\: y'=\pm \frac{3}{2}(x-1)^{\frac{1}{2}}.$$

(Знаки ± в выражении у указывают, что кривая симметрична оси $Ox$; точки $A$ и $B$, имеющие отрицательные ординаты, лежат на той ветви кривой, которая расположена ниже оси $Ox$.) Подставляя в формулу (1), получим

$$\displaystyle L_{AB}=\int_{x_{A}}^{x_{B}}\sqrt{1+(y')^{2}}dx=\int_{2}^{5}\sqrt{1+\frac{9}{4}(x-1)}dx=\frac{1}{2}\int_{2}^{5}\sqrt{9x-5}dx=\frac{1}{18}\int_{2}^{5}(9x-5)^{\frac{1}{2}}d(9x-5)=\frac{1}{27}(9x-5)^{\frac{3}{2}}\left.\begin{matrix} \\ \\ \end{matrix}\right| _{2}^{5}\approx 7,63.$$

2) Дифференцируем по $t$ параметрические уравнения циклоиды

$$\displaystyle \dot{x}=\frac{dx}{dt}=a(1-\cos t);\: \dot{y}=\frac{dy}{dt}=a\sin t$$

и находим дифференциал ее дуги

$$\displaystyle dl=\sqrt{\dot{x}^{2}+\dot{y}^{2}}dt=\sqrt{a^{2}(1-\cos t)^{2}+a^{2}\sin ^{2}t}dt=a\sqrt{2(1-\cos t)}dt=a\sqrt{4\sin ^{2}\frac{t}{2}}dt=2a\sin \frac{t}{2}dt.$$

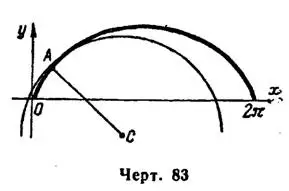
Рис. 3

Одна арка циклоиды (рис. 3) получается при изменении параметра $t$ от 0 до $2\pi$, поэтому

$$\displaystyle L=2a\int_{0}^{2\pi }\sin \frac{t}{2}dt=4a\int_{0}^{2\pi }\sin \frac{t}{2}d\frac{t}{2}=-4a\cos \frac{t}{2}\left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{2\pi}=8a.$$

3) Из данного уравнения кривой $\displaystyle \rho =\cos ^{3}\frac{\varphi }{3}$ находим производную $\displaystyle \rho' =\frac{d\rho }{d\varphi }=-a\cos ^{2}\frac{\varphi }{3}\sin \frac{\varphi }{3}$ и дифференциал ее дуги

$$\displaystyle dl=\sqrt{\rho ^{2}+(\rho ')^{2}}d\varphi =\sqrt{a^{2}\cos ^{6}\frac{\varphi }{3}+a^{2}\cos ^{4}\frac{\varphi }{3}\sin ^{2}\frac{\varphi }{3}}d\varphi =a\cos ^{2}\frac{\varphi }{3}d\varphi .$$

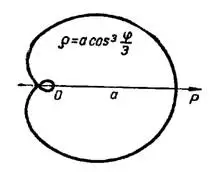
Рис. 4

Половина этой кривой, рис. 4, описывается концом полярного радиуса при изменении $\varphi$ от 0 до $\displaystyle \frac{3}{2}\pi$. Поэтому согласно формуле (2) длина всей кривой

$$\displaystyle L=2a\int_{0}^{\frac{3}{2}\pi }\cos ^{2}\frac{\varphi }{2}d\varphi =a\int_{0}^{\frac{3}{2}\pi }\left ( 1+\cos \frac{2\varphi }{3} \right )d\varphi =a\left ( \varphi +\frac{3}{2}\sin \frac{2\varphi }{3} \right )\left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{\frac{3}{2}\pi }=\frac{3}{2}a\pi.$$

Пример 2. Найти периметр фигуры, ограниченной кривыми $\displaystyle y^{3}=x^{2}$ и $\displaystyle y=\sqrt{2-x^{2}}$.
Решение. Совместно решая уравнения кривых, определим две точки их пересечения $A(1;1)$ и $B(-1;1)$. Построив эти точки и проходящие через них данные кривые, получим фигуру, симметричную оси $Oy$ (рис. 5).

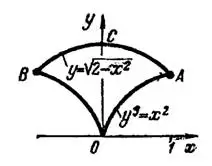
Рис. 5

Периметр этой фигуры $L=2(L_{\breve{OA}}+L_{\breve{AC}})$.
Пользуясь формулой (1), найдем:

$$\displaystyle L_{\breve{OA}}=\int_{y_{O}}^{y_{A}}\sqrt{1+\left ( \frac{dx}{dy} \right )^{2}}dy=\int_{0}^{1}\sqrt{1+\frac{9}{4}y}dy=\frac{4}{9}\int_{0}^{1}\left ( 1+\frac{9}{4}y \right )^{\frac{1}{2}}d\left ( 1+\frac{9}{4}y \right )=\frac{8}{27}\left ( 1+\frac{9}{4}y \right )^{\frac{3}{2}}\left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{1}=\frac{8}{27}\left ( \frac{13\sqrt{13}}{8}-1 \right );$$

$$\displaystyle L_{\breve{AC}}=\int_{x_{C}}^{x_{A}}\sqrt{1+(y')^{2}}dx=\int_{0}^{1}\sqrt{1+\frac{x^{2}}{2-x^{2}}}dx=\sqrt{2}\int_{0}^{1}\frac{dx}{\sqrt{2-x^{2}}}=\sqrt{2}\, \textrm{arcsin}\, \frac{x}{\sqrt{2}}\left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{1}=\frac{\pi \sqrt{2}}{4}.$$

(Это восьмая часть длины окружности, радиус которой $\sqrt{2}$.) Следовательно, искомый периметр фигуры

$$\displaystyle L=2\left ( \frac{13\sqrt{13}-8}{27}+\frac{\pi \sqrt{2}}{4} \right )\approx 5,102.$$