Площадь поверхности вращения. Практикум по математическому анализу. Урок 88

Если поверхность образуется при вращении дуги $AM$ плоской кривой вокруг оси $Ox$ (рис. 1), то дифференциал площади этой поверхности равен площади боковой поверхности усеченного круглого конуса с образующей $dl$ и радиусами оснований $y$ и $y+dy$:

$$\displaystyle ds=\frac{2\pi y+2\pi (y+dy)}{2}dl=\pi (2y+dy)dl\approx 2\pi y\, dl,$$

а площадь поверхности, образованной вращением дуги $AB$, определяется формулой

$$\displaystyle S=\int_{(A)}^{(B)}ds=2\pi \int_{(A)}^{(B)}y dl,\; \; \; \; \; \; (1)$$

где $(A)$ и $(B)$ обозначают значения в точках $A$ и $B$ выбранной переменной интегрирования, $dl$ —дифференциал дуги кривой.

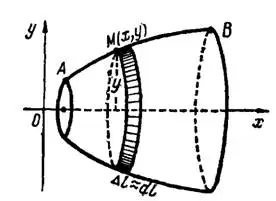
Рис. 1

При вращении дуги $AB$ кривой вокруг оси $Oy$ (рис. 2)

$$\displaystyle ds\approx 2\pi x\, dl;\; S=\int_{(A)}^{(B)}ds=2\pi \int_{(A)}^{(B)}x dl.\; \; \; \; \; (2)$$

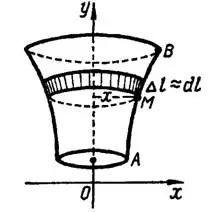
Рис. 2

Пример 1. Найти площадь поверхности, образованной вращением вокруг оси $Ox$: 1) дуги кубической параболы $\displaystyle y=x^{3}$, заключенной между прямыми $\displaystyle x=-\frac{2}{3}$ и $\displaystyle x=\frac{2}{3}$; 2) астроиды $\displaystyle x=a\cos ^{3}t,\: y=a\sin ^{3}t$; 3) эллипса

$$\displaystyle S=2\cdot 2\pi \int_{0}^{\frac{2}{3}}y\sqrt{1+(y')^{2}}dx=4\pi \int_{0}^{\frac{2}{3}}x^{3}\sqrt{1+9x^{4}}dx.$$

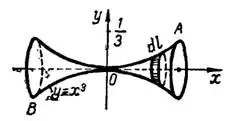
Рис. 3

Для вычисления интеграла полагаем $\displaystyle 1+9x^{4}=z$, тогда $\displaystyle 36x^{3}dx=dz;\: z_{1}=1$ при $\displaystyle x=0;\: z_{2}=\frac{25}{9}$ при $\displaystyle x=\frac{2}{3}$;

$$\displaystyle S=4\pi \int_{1}^{\frac{25}{9}}\sqrt{t}\frac{dt}{36}=\frac{\pi }{9}\int_{1}^{\frac{25}{9}}t^{\frac{1}{2}}dt=\frac{\pi }{9}\cdot \frac{2}{3}t^{\frac{3}{2}}\left.\begin{matrix} \\ \\ \end{matrix}\right| _{1}^{\frac{25}{9}}=\frac{2\pi }{27}\left ( \frac{125}{27}-1 \right )\approx 0,845.$$

2) Применяя формулу (1), преобразуя ее к переменной $t$, исходя из уравнений астроиды, получим

$$\displaystyle S=2\cdot 2\pi \int_{0}^{\frac{\pi }{2}}y\sqrt{x^{2}+y^{2}}dt=4\pi \int_{0}^{\frac{\pi }{2}}a\sin ^{3}t\sqrt{(-3a\cos ^{2}t\sin t)^{2}+(3a\sin ^{2}t\cos t)^{2}}dt=12a^{2}\pi \int_{0}^{\frac{\pi }{2}}\sin ^{4}t\cos tdt=12a^{2}\pi \int_{0}^{\frac{\pi }{2}}\sin ^{4}td\sin t=\frac{12}{5}a^{2}\pi \sin ^{5}t\left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{\frac{\pi }{2}}=\frac{12}{5}\pi a^{2}.$$

(Четвертая часть астроиды, расположенная в первом квадранте (рис. 4) получается при изменении $t$ от 0 до $\displaystyle \frac{\pi }{2}$.)

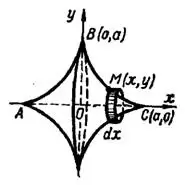
Рис. 4

3) Дифференцируя по $x$ обе части уравнения эллипса $\displaystyle \frac{2x}{a^{2}}+\frac{2yy'}{b^{2}}=0,\: yy'=-\frac{b^{2}x}{a^{2}}$ и подставляя в формулу (1), находим

$$\displaystyle S=2\pi \int_{-a}^{a}y\sqrt{1+(y')^{2}}dx=4\pi \int_{0}^{a}\sqrt{y^{2}+(yy')^{2}}dx=4\pi \int_{0}^{a}\sqrt{b^{2}-\frac{b^{2}x^{2}}{a^{2}}+\frac{b^{4}x^{2}}{a^{4}}}dx=\frac{4\pi b}{a}\int_{0}^{a}\sqrt{a^{2}-\frac{a^{2}-b^{2}}{a^{2}}x^{2}}dx=\frac{4\pi b}{a}\int_{0}^{a}\sqrt{a^{2}-\varepsilon ^{2}x^{2}}dx,$$

где $\displaystyle \varepsilon =\frac{\sqrt{a^{2}-b^{2}}}{a}=\frac{c}{a}$ — эксцентриситет эллипса.
Полагая $\displaystyle \varepsilon x=a\sin t$, получим $\displaystyle \varepsilon dx=a\cos t\, dt;\: t_{1}=0$ при $\displaystyle x=0;\: t_{2} =\textrm{arcsin}\, \varepsilon$ при $\displaystyle x=a$;

$$\displaystyle S=\frac{4\pi b}{a}\int_{0}^{t_{2}}\sqrt{a^{2}-a^{2}\sin ^{2}t}\, \frac{a}{\varepsilon }\cos t\, dt=\frac{4\pi ab}{\varepsilon }\int_{0}^{t_{2}}\cos ^{2}t\, dt=\frac{2\pi ab}{\varepsilon }\int_{0}^{t_{2}}(1+\cos 2t)dt=\frac{2\pi ab}{\varepsilon }\left ( t+\frac{1}{2}\sin 2t \right )\left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{t_{2}}=2\pi b\left ( b+\frac{a}{\varepsilon }\textrm{arcsin}\, \varepsilon \right ).$$

Отсюда при $\displaystyle \varepsilon \to 0$ получается площадь поверхности шара $\displaystyle S=4\pi a^{2}$.

Пример 2. Найти площадь поверхности, образованной вращением вокруг оси $Oy$: 1) дуги окружности $\displaystyle x^{2}+(y-b)^{2}=R^{2}$ между ее точками, где $\displaystyle y=y_{1}$ и $\displaystyle y=y_{2}$ 2) петли кривой $\displaystyle 9ax^{2}=y(3a-y)^{2}$.

Решение. 1) Если дуга данной окружности не пересекает оси $Oy$ (своего диаметра), то при вращении ее вокруг этой оси образуется поверхность, называемая сферическим поясом (рис. 5). Дифференцируя по $y$ обе части уравнения окружности $\displaystyle 2xx'+2(y-b)=0,\: xx'=-(y-b)$ и подставляя в формулу (2), получим

$$\displaystyle S=2\pi \int_{y_{1}}^{y_{2}}x\sqrt{1+(x')^{2}}dy=2\pi \int_{y_{1}}^{y_{2}}\sqrt{x^{2}+(xx')^{2}}dy=2\pi \int_{y_{1}}^{y_{2}}\sqrt{R^{2}-(y-b)^{2}+(y-b)^{2}}dy=2\pi R\int_{y_{1}}^{y_{2}}dy=2\pi R(y_{2}-y_{1})=2\pi RH,$$

где $H$ — высота пояса. При $H=2R$ получим формулу площади сферы $\displaystyle S=4\pi R^{2}$.

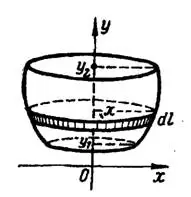
Рис. 5

2) Петля данной кривой (рис. 6) описывается текущей точкой при изменении $y$ от 0 до $3a$. Поэтому, дифференцируя по $y$ обе части ее уравнения: $\displaystyle 18axx'=(3a-y)^{2}-2y(3a-y)=3(3a-y)(a-y),\: xx'=\frac{(3a-y)(a-y)}{6a}$ и подставляя в формулу (2), получим

$$\displaystyle S=2\pi \int_{0}^{3a}\sqrt{x^{2}+(xx')^{2}}dy=2\pi \int_{0}^{3a}\sqrt{\frac{y(3a-y)^{2}}{9a}+\frac{(3a-y)^{2}(a-y)^{2}}{36a^{2}}}dy=2\pi \int_{0}^{3a}\frac{3a-y}{6a}\sqrt{a^{2}+2ay+y^{2}}dy=\frac{\pi }{3a}\int_{0}^{3a}(3a^{2}+2ay-y^{2})dy=3\pi a^{2}.$$

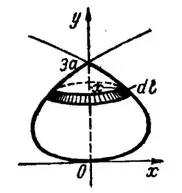
Рис. 6