Вероятность суммы событий. Решение типовых задач

Вероятность суммы событий. Решение типовых задач

Событие А + В называют суммой событий А и В, если А+В происходит, когда происходит хотя бы одно из событий: А или В. Вероятность суммы А+В равна сумме вероятностей А и В,

$$P(A+B)=P(A)+P(B),\; \; \; (1)$$

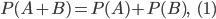
если события А и B несовместны, т. е. А и В не могут произойти одновременно, в общем случае

$$P(A+B)=P(A)+P(B)-P(AB).\; \; \; (2)$$

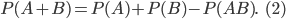
Здесь произведение событий АВ — это событие, состоящее в том, что происходит и событие А, и событие B. Если А и В несовместны, то АВ — невозможное событие. Тогда Р(AB) = 0 и из (2) следует (1).
Если использовать задание случайных событий посредством перечисления благоприятствующих элементарных событий, то суммой событий А+В нужно назвать событие, состоящее из элементарных событий, каждое из которых входит хотя бы в одно из событий А или В; произведение АВ состоит из элементарных событий, входящих и в A, и в B.
Событие 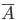$\bar{A}$, противоположное событию А, состоит в том, что А не произошло. Формула

$$P(A)=1-P(\bar{A})\; \; \; (3)$$

оказывается полезной в тех случаях, когда вероятность события 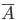$\bar{A}$ вычислить проще, чем вероятность события А.
Если среди событий $A_{1},A_{2},...,A_{n}$ любые два события несовместны, то

$$P(A_{1}+A_{2}+...+A_{n})=P(A_{1})+P(A_{2})+...+P(A_{n}).\; \; \; (4)$$

Задача №1. Брошено две игральных кости. Найти вероятность события D = {выпала хотя бы одна «шестерка»}.
Решение. 1-й способ. Элементарным событием является пара чисел (i, j): і — число очков, выпавших на 1-й кости, j — число очков, выпавших на 2-й кости. Поскольку при любом значении i (i=1, ..., 6) число j может принять любое из 6 возможных значений, то каждому фиксированному і соответствует 6 элементарных событий: (i, 1), (i, 2), ..., (i, 6); таким образом, $\Omega$ = {(1, 1), (1, 2), ..., (1, 6); (2, 1), ..., (2, 6); (3, 1), ..., (6, 6)} и $\left |\Omega \right |$ = 6·6 = 36.
Пусть $E_{1}$ = {на 1-й кости выпала «шестерка»}, $E_{2}$ = {на 2-й кости выпала «шестерка»}. Тогда $D=E_{1}+E_{2}$. Заметим, что события $E_{1}$ и $E_{2}$ не являются несовместными, так как $E_{1}$ и $E_{2}$ могут произойти одновременно:
$E_{1}E_{2}$= {на обеих костях выпала «шестерка»} = (6, 6).
Таким образом, $E_{1}E_{2}$ происходит при единственном элементарном событии $(\left|E_{1}E_{2} \right|=1)$; $E_{1}$ и $E_{2}$ происходят при 6 элементарных событиях $(\left|E_{1} \right|=\left|E_{2} \right|=6)$. По формуле

$$P(A)=\frac{|A|}{|\Omega |}=\frac{K}{S}.\; \; \; (*)$$

$P(E_{1})=P(E_{2})=\frac{6}{36}=\frac{1}{6},\; P(E_{1}E_{2})=\frac{\left|E_{1}E_{2} \right|}{\left| \Omega\right| }=\frac{1}{36}.$
Используя эти значения, по формуле (2) найдем вероятность события $D=E_{1}+E_{2}$:

$$P(D)=P(E_{1})+P(E_{2})-P(E_{1}E_{2}) =\frac{1}{6}+\frac{1}{6}-\frac{1}{36}=\frac{11}{36}.$$

2-й способ. Заметим, что событие D противоположно событию С: $\bar{D}=C=${не выпала ни одна «шестерка»}. Событие С состоит из всех элементарных событий (i, j), в которых $i\neq 6,\; j\neq 6$:
С={(i, j): i,j=1,2,3,4,5}. Нетрудно проверить, что |С|=25. По формуле (*)

$$P(C)=\frac{|C|}{|\Omega |}=\frac{25}{36}.$$

Отсюда, привлекая формулу (3), получаем

$$P(D)=1-P(\bar{D})=1-P(C)=1-\frac{25}{36}=\frac{11}{36}.$$

Задача №2. В ящике 10 одинаковых карточек, на которых по одной написаны цифры О, 1, ..., 9. Два раза с возвращением вынимается по одной карточке. Найти вероятности событий:
А = {на вьшутых карточках появились цифры «О», «О»},
B = {на 2-й карточке появилась «9»},
С={ни на одной вынутой карточке не было «5»},
D = {появилась хотя бы одна «1»}.
Ответ: Р(A) = 0,01, P(B) = 0,l, Р(С) = 0,81, P(D) = 0,19.
Задача №3. В телефонном номере три последние цифры стерлись. Считая, что все возможные значения стершихся цифр равновероятны, найти вероятности событий:
A = {стерлись различные цифры},
B = {стерлись одинаковые цифры},
С = {среди стершихся цифр хотя бы две совпадают},
D = {среди стершихся цифр хотя бы две различны}.
Ответ: $P(A)=\frac{10\cdot 9\cdot 8}{10^{3}}=0,72;\; P(B)=\frac{10}{10^{3}}=0,01;\; P(C)=P(\bar{A})=0,28;\; P(D)=0,99.$