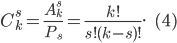Классическое определение вероятности. Формулы теории соединений

Классическое определение вероятности

Вероятность события А равна

$$P(A)=\frac{m}{n}.\; \; \; \; (1)$$

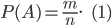
В этой формуле m — число исходов испытания, благоприятствующих событию А; n - число всех равновозможных несовместных исходов испытания, образующих полную группу.
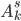При вычислении вероятностей пользуются формулами теории соединений. Основными из них являются формулы для определения: $P_{k}$ - числа перестановок из k элементов, $A_{k}^{s}$ - числа размещений из k элементов по s и 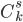$C_{k}^{s}$ - числа сочетаний из k элементов по s. Число перестановок из k элементов равно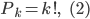

$$P_{k}=k!,\; \; \; \; (2)$$

где 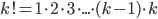$k!=1\cdot 2\cdot 3\cdot ...\cdot (k-1)\cdot k$. Принято,что 0! = 1.
Число размещений из k элементов по s равно

$$A_{k}^{s}=k\cdot (k-1)\cdot (k-2)\cdot ...\cdot (k-s+1).\; \; \; \; (3)$$

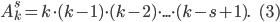
Число сочетаний из k элементов по s равно

$$C_{k}^{s}=\frac{A_{k}^{s}}{P_{s}}=\frac{k!}{s!(k-s)!}.\; \; \; \; (4)$$