При изучении поведения функции в зависимости от изменения независимой переменной обычно предполагается, что во всей области определения функции независимая переменная изменяется монотонно возрастая, т. е. что каждое следующее ее значение больше предыдущего.
Если при этом последовательные значения функции также возрастают, то и функция называется возрастающей, а если они убывают, то и функция называется убывающей.
Некоторые функции во всей своей области определения изменяются монотонно — только возрастают или только убывают (например  ).
).
Многие функции изменяются не монотонно. В одних интервалах изменения независимой переменной они возрастают, а в других интервалах убывают (например,  ).
).
Возрастание и убывание функции  характеризуется знаком ее производной
характеризуется знаком ее производной  : если в некотором интервале , то функция возрастает, а если
: если в некотором интервале , то функция возрастает, а если  , то функция убывает в этом интервале.
, то функция убывает в этом интервале.
Пример 1. Определить интервалы возрастания и убывания следующих функций:
1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Решение. 1) Производная —  положительна при
положительна при
 и и отрицательна при
и и отрицательна при  и при
и при  . Учитывая, что область определения функции
. Учитывая, что область определения функции  есть интервал
есть интервал  , заключаем: в интервале
, заключаем: в интервале  функция
функция  возрастает, а в интервале
возрастает, а в интервале  она убывает.
она убывает.
2) Функция  определена в полуоткрытом интервале
определена в полуоткрытом интервале  ; ее производная — во всем этом интервале. Поэтому функция
; ее производная — во всем этом интервале. Поэтому функция  монотонная, она возрастает во всей своей области определения.
монотонная, она возрастает во всей своей области определения.
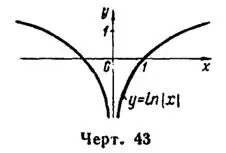
3) Функция  определена на всей числовой оси, исключая точку
определена на всей числовой оси, исключая точку  ; ее производная при при
; ее производная при при  . Отсюда следует, что функция
. Отсюда следует, что функция  убывает в интервале
убывает в интервале  и возрастает в интервале
и возрастает в интервале  . График этой четной функции приведен на рис. 43.
. График этой четной функции приведен на рис. 43.
Возрастание и убывание функции. Практикум по математическому анализу. Урок 51







