Функция у = f(x) называется четной, если для любых х и (—х) из области определения функции выполняется равенство f(-x) = f(x).
Функция y = f(x) называется нечетной, если для любых х и (—х) из области определения функции выполняется равенство f(—х) = — f(x). Если функция у = f(x) такова, что хотя бы для одной пары значений х и (—х) оказалось, что f(-x) ≠-f(x), и хотя бы для одной пары значений х и (-х) оказалось, что f(-x) ≠ f(x), то функция называется функцией общего вида. Кратко: если
![]()
то f(x) — функция общего вида.
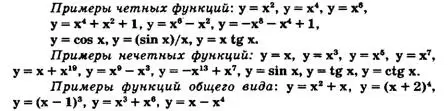
Из определения четных и нечетных функций следует, что область определения D(f) как четной, так и нечетной функции симметрична относительно начала координат, если
х∈ D(f)=>(-x)∈ D(f).
Если функция у = f(x) является четной, то ее график симметричен относительно оси ординат.
Если функция у = f(x) является нечетной, то ее график симметричен относительно начала координат.
Пример. Выяснить, является ли данная функция четной, нечетной, общего вида:
![]()
![]()
Решение.
![]()
— четная функция;
![]()
— четная функция;
![]()
— нечетная функция;
![]()
![]()
— нечетная функция;
![]()
![]()
— функция общего вида;
![]()
— функция общего вида.
Ответ: а), б) — четные функции; в), г) — нечетные функции; д), е) — функции общего вида.
Четные и нечетные функции






