Двучленные и трехчленные уравнения

Алгебраическое уравнение называется двучленным уравнением, если оно имеет вид xⁿ-a = 0 (n∈N).
В простейшем случае при а=1 имеем хⁿ -1 = 0 Тогда
а) при n= 1 имеем х - 1 = 0 <=> х = 1;
б) при n=2 имеем х² -1 = 0 <=> (х - 1)(х +1) = 0 <=> x₁ =1, х₂ = -1;
в) при n=3 имеем х³ -1 = 0 <=> (х -1)(х² + x + l) = 0<=>x = 1 — единственный действительный корень.
Можно показать, что в общем случае для двучленных уравнений хⁿ - а = 0 справедливы следующие утверждения:
1) при любом положительном а уравнение хⁿ - а = 0 имеет:
а) при любом нечетном n (n = 2k-1, k∈N) только один действительный корень
б) при любом четном n (n = 2k, k∈N) только два действительных корня
2) при а=0 уравнение хⁿ - а = 0 имеет только один корень х=0;
3) при любом отрицательном а уравнение хⁿ-а=0 имеет:
а) при любом нечетном n (n = 2k-1, k∈N) только один действительный корень
б) при любом четном n (n = 2k, k∈N) не имеет действительных корней.
Пример 1. Решить уравнение

Решение.

Ответ: {-5;5}
Пример 2. Решить уравнение х³ - 27 = 0.
Решение.

Ответ: {3}.
Пример 3. Решить уравнение х⁵ -12 = 0.
Решение.

Ответ: {⁵√12}
Пример 4. Решить уравнение х² + 4 = 0.
Решение.
x² + 4 = 0 <=> x² = -4 <=> x є 0 .
Ответ: ∅.
Пример 5. Решить уравнение x⁶+ 123 = О
Решение.

Ответ: ∅.
Пример 6. Решить уравнения: a) x³=0; б) x¹²=0.
Решение.

Алгебраическое уравнение вида ах²ⁿ + Ьхⁿ + с = 0 называется трехчленным, если n≥2, n∈N, а≠0, Ь≠0, с≠0.
При n=2 трехчленное уравнение ах⁴ + Ьх² + с = 0 называется биквадратным уравнением.
Заменой переменной xⁿ=t трехчленное уравнение ах²ⁿ + Ьхⁿ + с = 0 преобразуется в квадратное at² + bt + с = 0.
В частности, для биквадратного уравнения замена х² = t приводит его к квадратному уравнению at² + bt + с = 0.
Пример 1. Решить уравнение x⁴-13x²+36=0.
Решение.
Имеем биквадратное уравнение. Положив x²=t, получим квадратное уравнение t²-13t + 36 = 0 <=> t₁ = 4, t₂ = 9 Задача свелась к решению уравнений x² =4 <=> x₁,₂ =±2; x² =9 <=> х₃,₄ =±3.
Ответ: {±2;±3}.
Пример 2. Решить уравнение х⁴-3x²-10=0.
Решение.
Положив x² = t, получаем квадратное уравнение t²-3t-10 = 0 <=> t₁ =-2, t₂ =5.
Теперь задача сводится к решению уравнений х² = -2, х² = 5. Уравнение х² =-2 не имеет действительных корней, уравнение х² = 5 имеет два корня x₁ =-√5, х₂=√5 .
Ответ: {±√5}.
Пример 3. Решить уравнение x⁶-3x³+2=0.
Решение.
Имеем трехчленное уравнение. Положив x³=t, получаем
x⁶=(x³)²=t²,

Ответ: {1;³√2}.
Пример 4. Решить уравнение x⁸-17x⁴+16=0
Решение.
Положив х⁴ = t, получаем


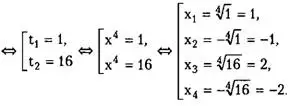
Ответ: {± 1; ± 2}