Теорема Виета формулируется следующим образом: если приведенное квадратное уравнение х² + рх + q = 0 имеет действительные корни х1 и х2, то их сумма равна (-р), а произведение равно q, т. е.
![]()
Таким образом, сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Замечание. Поскольку неприведенное квадратное уравнение всегда можно сделать приведенным, разделив его обе части на коэффициент при х², то теорема Виета для неприведенного квадратного уравнения имеет вид
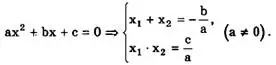
Из теоремы Виета для неприведенного квадратного уравнения следует, что квадратный трехчлен может быть разложен на линейные множители следующим образом:
ах² + bх + с = а(х-х1)(х-х2),
где х1,х2 — корни уравнения ах² + bх + с = 0.
Теорема Виета






