Геометрическая прогрессия (основные формулы)

Геометрической прогрессией называется такая числовая последовательность 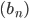$(b_{n})$, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же постоянное для данной последовательности число, отличное от нуля. Первый член геометрической прогрессии предполагается отличным от нуля. 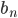$b_{n}$ называется $n$ - ым членом геометрической прогрессии.
Примеры геометрической прогрессии:
а) 1;2;4;8;16;32;...;
б) 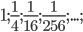$1;\frac{1}{4};\frac{1}{16};\frac{1}{256};...;$
в) 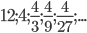$12;4;\frac{4}{3};\frac{4}{9};\frac{4}{27};...$.
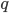Из определения геометрической прогрессии следует, что $q=\frac{b_{n+1}}{b_{n}}$. Число $q$ называется знаменателем геометрической прогрессии. Таким образом,
$q=\frac{b_{2}}{b_{1}}=\frac{b_{3}}{b_{2}}=\frac{b_{4}}{b_{3}}=...=\frac{b_{n+1}}{b_{n}}=...$
Для того чтобы задать геометрическую прогрессию 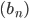$(b_{n})$, достаточно знать ее первый член и знаменатель.
Если

$$b_{n}=\sqrt{b_{n-1}\cdot b_{n+1}}\Rightarrow b_{n}^{2}=b_{n-1}\cdot b_{n+1};$$

б) произведение членов, равноотстоящих от концов геометрической прогрессии, есть величина постоянная, т. е.

$$b_{1}\cdot b_{n}=b_{2}\cdot b_{n-1}=b_{3}\cdot b_{n-2}=...$$

Формула $n$-го члена геометрической прогрессии имеет вид

$$b_{n}=b_{1}q^{n-1}.$$

Фурмулы для суммы $n$ первых членов геометрической прогрессии имеют вид

$$S_{n}=\frac{b_{1}-b_{n}q}{1-q}=\frac{b_{1}\left ( 1-q^{n} \right )}{1-q}.$$