Пример 1. В геометрической прогрессии 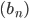
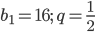 . Найти
. Найти 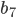 .
.
Решение.
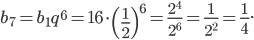
Ответ: 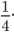
Пример 2. Дана геометрическая прогрессия 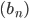 : 2;-6;18. Найти
: 2;-6;18. Найти 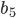 .
.
Решение.
Найдем сначала знаменатель прогрессии:

Ответ: 162.
Пример 3. Найти первый член геометрической прогрессии
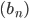 , если
, если 
Решение.

0твет:

Пример 4. В геометрической прогрессии
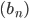 :
: 
Найти
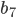 .
.Решение.
 . Найдем знаменатель прогрессии
. Найдем знаменатель прогрессии 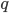 . Имеем:
. Имеем:

Ответ: -162.
Пример 5. В геометрической прогрессии
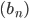 :
: 
Найти
 .
.Решение.
Найдем сначала знаменатель прогрессии
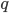 . По условию
. По условию

Ответ: 96.






