Пример 1. В геометрической прогрессии 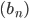 :
: 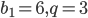 . Найти
. Найти 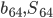
Решение.
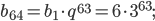
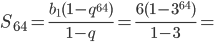
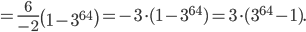
Ответ: 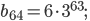
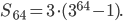
Пример 2. Найти сумму 
Решение.
Имеем 
Отсюда искомая сумма есть 
Ответ: 
Пример 3. В геометрической прогрессии 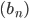 :
: 
Найти сумму  восьми первых членов прогрессии.
восьми первых членов прогрессии.
Решение.
Поскольку 
то имеем систему уравнений, равносильную исходной: 
Разделив почленно второе уравнение на первое, получим 
Из первого уравнения системы 
Итак,  По формуле для суммы
По формуле для суммы  первых членов находим
первых членов находим

Ответ:







