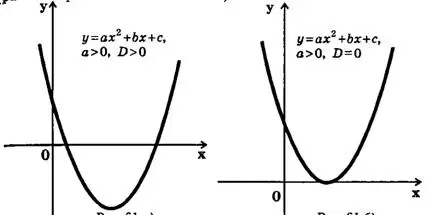
Графическое решение неравенств второй степени
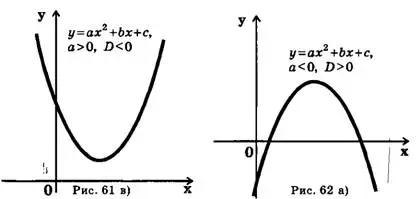
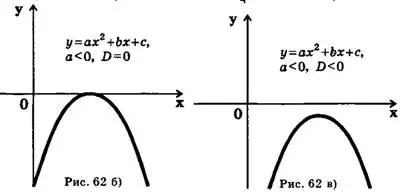
Как известно, графиком квадратичной функций 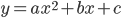 является парабола с ветвями, направленными вверх, если , и вниз, если
является парабола с ветвями, направленными вверх, если , и вниз, если  (иногда говорят, что парабола направлена выпуклостью вниз, если и выпуклостью вверх, если
(иногда говорят, что парабола направлена выпуклостью вниз, если и выпуклостью вверх, если  ). При этом возможны три случая: парабола пересекает ось Ox (т. е. уравнение
). При этом возможны три случая: парабола пересекает ось Ox (т. е. уравнение 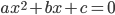 имеет два различных корня), парабола имеет вершину на оси Ox (т. е. уравнение
имеет два различных корня), парабола имеет вершину на оси Ox (т. е. уравнение 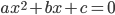 имеет один корень, так называемый двукратный корень), парабола не пересекает ось Ox (т. е. уравнение
имеет один корень, так называемый двукратный корень), парабола не пересекает ось Ox (т. е. уравнение 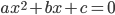 не имеет действительных корней). Таким образом, возможны шесть положений параболы, которые представлены на рис.1—2 (
не имеет действительных корней). Таким образом, возможны шесть положений параболы, которые представлены на рис.1—2 (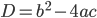 — дискриминант квадратного трехчлена
— дискриминант квадратного трехчлена 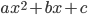 ).
).
Используя графические иллюстрации, можно решать квадратные неравенства. График параболы можно строить чисто схематически, не находя координаты вершин (если  ) и точку пересечения с осью
) и точку пересечения с осью  .
.
Пример 1. Решить неравенство .
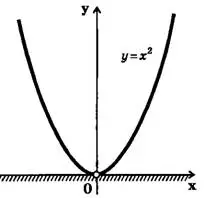
Решение. Рассмотрим функцию  . Графиком этой функции является парабола, ветви которой направлены вверх (парабола направлена выпуклостью вниз). Парабола пересекает ось
. Графиком этой функции является парабола, ветви которой направлены вверх (парабола направлена выпуклостью вниз). Парабола пересекает ось  в точке с абсциссой
в точке с абсциссой  , так как
, так как  <=>
<=>  . Изобразив схематически параболу
. Изобразив схематически параболу  (рис. 3), найдем, что при
(рис. 3), найдем, что при  . На чертеже искомое множество заштриховано.
. На чертеже искомое множество заштриховано.
Ответ:  .
.
Пример 2. Решить неравенство  .
.
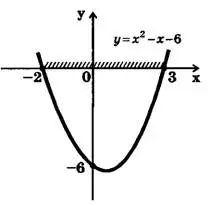
Решение. Рассмотрим функцию  . Графиком этой функции является парабола, ветви которой направлены вверх, т. к. . Решим уравнение
. Графиком этой функции является парабола, ветви которой направлены вверх, т. к. . Решим уравнение  . Корни его
. Корни его  . Значит данная парабола
. Значит данная парабола  пересекает ось
пересекает ось  в точках с абсциссами
в точках с абсциссами  . Изобразив схематически параболу
. Изобразив схематически параболу  (рис.4), находим, что
(рис.4), находим, что  , если
, если ![x\in \left[-2;3 \right]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_e3222b28e9cfb0370df1df697b5478de.gif) . Искомое множество заштриховано на рис.4.
. Искомое множество заштриховано на рис.4.
Ответ: ![x\in \left[-2;3 \right]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_e3222b28e9cfb0370df1df697b5478de.gif) .
.
Пример 3. Решить неравенство .
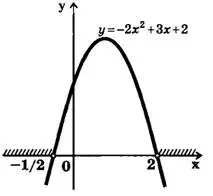
Решение. Рассмотрим функцию  . Ее графиком является парабола, ветви которой направлены вниз (парабола направлена выпуклостью вверх), т. к.
. Ее графиком является парабола, ветви которой направлены вниз (парабола направлена выпуклостью вверх), т. к.  .
.

 , находим, что
, находим, что  в каждом из бесконечных промежутков:
в каждом из бесконечных промежутков:  . Искомое множество заштриховано на рис.5.
. Искомое множество заштриховано на рис.5.Ответ:
 .
.Пример 4. Решить неравенство
 .
.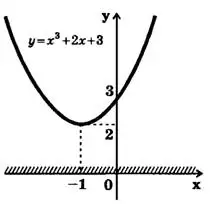
Решение. Поскольку для квадратного трехчлена  дискриминант
дискриминант  , то парабола
, то парабола  не пересекает ось
не пересекает ось  . Изобразив параболу
. Изобразив параболу  схематически (рис.6), находим, что при любом значении
схематически (рис.6), находим, что при любом значении  . Искомое множество заштриховано на рис.6.
. Искомое множество заштриховано на рис.6.
Ответ:  .
.