Неравенства второй степени

Неравенства второй степени
Пусть требуется решить неравенство $ax^{2}+bx+c>0$ (аналогичные рассуждения проводятся при решении неравенств 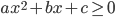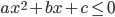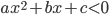$ax^{2}+bx+c\geq0$ , $ax^{2}+bx+c\leq0$ , $ax^{2}+bx+c<0$ ). В зависимости от знака дискриминанта квадратного трехчлена 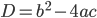$D=b^{2}-4ac$ нужно рассмотреть два случая.
1) Если 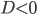$D<0$ , а старший коэффициент а положителен, то при всех значениях $x$ выполняется неравенство $ax^{2}+bx+c>0$ .
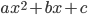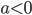2) Если $D>0$ , то для решения неравенства $ax^{2}+bx+c>0$ нужно разложить квадратный трехчлен $ax^{2}+bx+c$ на множители по формуле $ax^{2}+bx+c=a(x-x_{1})(x-x_{2})$ , затем разделить обе части неравенства $a(x-x_{1})(x-x_{2})>0$ на число $a$ , сохранив знак неравенства, если $a>0$ , и изменив знак неравенства на противоположный, если $a<0$ , и перейти к неравенству $(x-x_{1})(x-x_{2})>0$ . Дальше используют тот факт, что произведение двух чисел положительно, если сомножители имеют одинаковые знаки если $(x-x_{1})(x-x_{2})<0$ , то сомножители имеют противоположные знаки).

Пример 1. Решить неравенство $x^{2}-5x+6>0$ .
Решение.

$x^{2}-5x+6=0 \Leftrightarrow x_{1}=2,x_{2}=3 \Rightarrow x^{2}-5x+6=(x-2)(x-3).$

Отсюда

$x^{2}-5x+6>0\Leftrightarrow (x-2)(x-3)>0 \Leftrightarrow$

$\Leftrightarrow \left[ \begin{matrix} \left\{\begin{matrix} x-2>0,\\ x-3>0, \end{matrix}\right.\\ \left\{\begin{matrix} x-2<0,\\ x-3<0 \end{matrix}\right. \end{matrix} \right. \Leftrightarrow \left[ \begin{matrix} \left\{\begin{matrix} x>2,\\ x>3, \end{matrix}\right.\\ \left\{\begin{matrix} x<2,\\ x<3 \end{matrix}\right. \end{matrix} \right. \Leftrightarrow \left[ \begin{matrix} x>3,\\ x<2 \end{matrix} \right. \Leftrightarrow x \in (-\propto ;2)\bigcup (3;\propto )$

Ответ:

$x \in (-\propto ;2)\bigcup (3;\propto ).$

Пример 2. Решить неравенство $2x^{2}-x-1 \leq 0$ .
Решение. $2x^{2}-x-1=0\Leftrightarrow x_{1}=1,\: x_{2}=-\frac{1}{2}.$
Отсюда $2x^{2}-x-1=2(x-1)\left( x+\frac{1}{2}\right)$ и, следовательно,

$2x^{2}-x-1\leq 0 \Leftrightarrow 2(x-1)\left( x+\frac{1}{2}\right) \leq 0 \Leftrightarrow (x-1)\left(2 x+1\right) \leq 0$

$\Leftrightarrow \left[ \begin{matrix} \left\{\begin{matrix} x-1\leq 0,\\ x+\frac{1}{2}\geq 0, \end{matrix}\right.\\ \left\{\begin{matrix} x-1\geq 0,\\ x+\frac{1}{2}\leq 0 \end{matrix}\right. \end{matrix} \right. \Leftrightarrow \left[ \begin{matrix} \left\{\begin{matrix} x\leq 1,\\ x\geq -\frac{1}{2}, \end{matrix}\right.\\ \left\{\begin{matrix} x\geq 1,\\ x\leq -\frac{1}{2} \end{matrix}\right. \end{matrix} \right. \Leftrightarrow \left[ \begin{matrix} -\frac{1}{2}\leq x\leq 1,\\ x\in \oslash \end{matrix} \right. \Leftrightarrow -\frac{1}{2}\leq x\leq 1.$

Ответ: $x\in \left[-\frac{1}{2};1 \right].$
Замечание. Рассмотренные выше неравенства второй степени обычно решают либо графически, либо методом интервалов, которые рассмотрены ниже. Однако приведенные выше способы также имеют право на существование, т. к. они достаточно просты и наглядны.