Функция √x и ее график
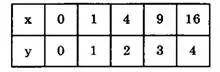
Составим таблицу некоторых значений, учитывая, что функция определена при х≥0 (табл. 1).
Таблица 1
Строим график функции у = √x (рис. 1).
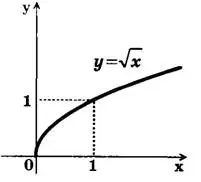
Свойства функции у=√x
а) D(f)=[0;+∞) ;
б) E(f)=[0;+∞);
в) функция у = √x имеет один нуль: у=0 при х=0;
г) функция принимает положительные значения при хє(0;+∞);
д) функция возрастает при хє(0;+∞);
е) функция имеет минимум при х=0, min у=у(0)=0;
ж) функция у = √x ни четная, ни нечетная, то есть у = √x является функцией общего вида.
Функция у = ³√x и ее график
Составим таблицу (табл. 2).
Таблица 2
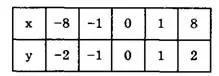
Строим график функции у = ³√x (рис. 2).
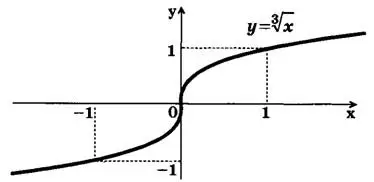
Свойства функции у = ³√x
а) D(f) = (-∞;+∞);
б) E(f)=(-∞;+∞);
в) функция имеет один нуль: у=0 при х=0;
г) функция принимает положительные значения при х є (0;+∞); функция принимает отрицательные значения при х є (-∞;0);
д) функция возрастает при хє (-∞;;+∞), т.е. на всей области определения;
е) функция не имеет экстремумов;
ж) у(-х)=-у(х) =>; функция у = ³√x нечетная, ее график симметричен относительно начала координат.
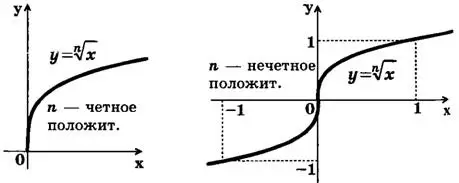
Функция у = ⁿ√x и ее график
При четном n функция у = ⁿ√x обладает теми же свойствами, что и функция у = √x, и график ее напоминает график функции у = √x. При нечетном n функция у = ⁿ√x обладает теми же свойствами, что и функция у = ³√x, и график ее напоминает график функции у = ³√x . На рис. 3, 4 изображены графики функций у = ⁿ√x при n четном и n нечетном