Функция у = х³ и ее график
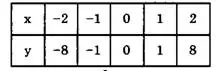
Составим таблицу значений функции (табл. 1).
Таблица 1
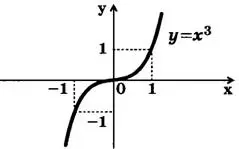
Графиком функции у = х³ является кубическая парабола (рис. 1).
Свойства функции у=х³:
а) D(f)=R;
б) E(f)=R;
в) функция имеет один нуль: у=0 при х=0;
г) функция принимает отрицательные значения при х ∈ (-∞;0), функция принимает положительные значения при х ∈ (0,+∞);
д) функция возрастает на всей области определения;
е) функция не имеет экстремумов;
ж) у(-х)=-у(х) => функция у = х³ нечетная, ее график симметричен относительно начала координат.
В более общем виде можно рассмотреть степенную функцию с натуральным показателем.
Степенная функция с натуральным показателем
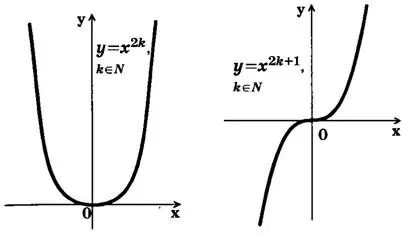
Рассмотрим функцию у = хⁿ, где n∈N, x∈R. При n=1 получаем у=х — линейную функцию. Пусть теперь n>1. Если n — четное натуральное число (n=2k, k∈N)» то свойства функции у = хⁿ такие же, как и у функции у = х².
Если n нечетное натуральное число, большее или равное 3 (n=2k+1, k∈N), то свойства функции такие же, как и у функции у = х³. Поэтому приведем общий вид графиков функций (рис. 2, 3).
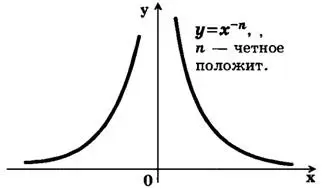
Степенная функция с целым отрицательным показателем (у = хˉⁿ, n∈N )
Рассмотрим функцию у = хˉⁿ, где n є N. При n=1 получаем y = xˉ¹=1/x — гипербола. Пусть n — нечетное число, большее единицы (n=3, 5, 7, 9, ...). В этом случае функция у = хˉⁿ обладает в основном теми же свойствами, что и функция у=1/х. График функции y = хˉⁿ (n=2k+1, k є N) напоминает график функции у=1/х (рис. 4).
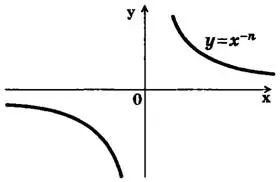
Пусть n четное число (n=2k, k є N). Перечислим некоторые свойства функции y=xˉ²=1/x²:
а) D(f)=(-∞;0) и (0;+∞)=R\{0};
б) E(f)=(0;+∞)
в) у(—х)=у(х) => y=1/x²— четная функция;
г) у = — убывает при х є (0;+∞) и возрастает при х є (-∞;0).
Такими же свойствами обладают любые функции вида у = хˉⁿ при четном n, большем двух. График функций у = хˉⁿ (общий вид графиков функций у = хˉⁿ при четном положительном n) изображен на рис. 5.