Функция, заданная формулой у = ах² + bх + с, где а, b, с — заданные числа (а≠0), называется квадратичной. Область определения квадратичной функции D(y) = R. Графиком функции у = ах² + bх + с является парабола. Если а>0, то ветви параболы направлены вверх; если а<0, то ветви направлены вниз. Прямая x=-b/a — является осью симметрии.
Для построения графика функции у = ах² + bх + с ее приводят к виду у = а(х + m)² + р путем выделения полного квадрата. Полный квадрат выделяется следующим образом:
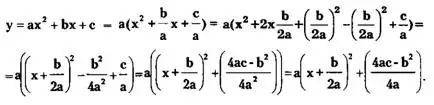
Таким образом, у = ах² +bx + c=a(x + m)² +р, где m = b/a, p=(4ac-b²)/4a. Точка с координатами (-m;p) есть
вершина параболы.
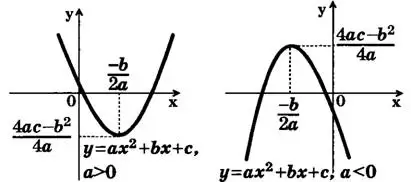
На рис. 1, 2 приведены параболы для а>0 и а<0
Рассмотрим более подробно функцию у = x².
Функция у=х²
Составим таблицу некоторых значений функции (табл. 1).
Таблица 1
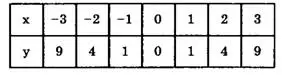
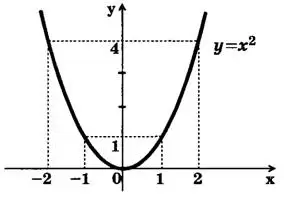
График функции у = х² есть парабола, вершина которой совпадает с началом координат, а ветви параболы направлены вверх (рис. 3).
Свойства функции у = х²:
а) D(f)=R;
б) E[0;+∞);
в) функция имеет один нуль: у=0 при х=0;
г) функция принимает положительные значения при хєR\{0}=(-∞;0)и(0;+∞);
д) функция возрастает при х є (0;+∞), функция убывает при х є (-∞;0)
е) функция имеет минимум при х=0 (min у=у(0)=0);
ж) у(-х)=у(х) => функция у = х² четная, ее график симметричен относительно оси Оу.






