Квадратные уравнения
Уравнение вида ах² + Ьх + с = 0 (а≠0) называется квадратным уравнением с одной переменной. а — коэффициент при х² (первый коэффициент ), b — коэффициент при х (второй коэффициент), с — свободный член.
Если b≠0, с≠0, то квадратное уравнение называется полным. Если а=1, то квадратное уравнение называется приведенным, если а≠1,— неприведенным. Неприведенное квадратное уравнение всегда можно сделать приведенным, разделив обе части его на первый коэффициент а≠0.
![]()
— приведенное квадратное уравнение.
Приведенные квадратные уравнения обычно записываются в виде х² + рх + q = 0.
Корни квадратного уравнения можно найти, выделяя полный квадрат двучлена из квадратного трехчлена:
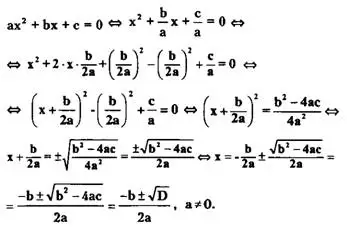
Таким образом, корни квадратного уравнения ах² + Ьх + с = О находят по формуле
![]()
где D = Ь² - 4ас называется дискриминантом квадратного уравнения ах² + Ьх + с = 0.
Если D<0, то уравнение ах² + Ьх + с = 0 не имеет действительных корней; если D=0, то
![]()
и уравнение ах² + Ьх + с = 0 имеет равные корни (в этом случае говорят, что уравнение имеет кратный корень кратности два); если D>0, то уравнение ах² + Ьх + с = 0 имеет два различных действительных корня. Итак,
![]()
Если b=2k (b — четное число, k є Z), то формулу для нахождения корней можно упростить:
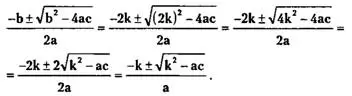
Итак, если квадратное уравнение имеет вторым коэффициентом четное число, то имеем уравнение
![]()
Пример 1. Решить уравнение 2х² -5х + 2=0.
Решение.
Имеем а=2; Ь=-5; с=2 =>
![]()
![]()
Ответ: {2; 1/2}.
Пример 2. Решить уравнение 5х² - 18х + 9 = 0.
Решение.
Применяем формулу для нахождения корней квадратного уравнения, когда коэффициент при х — четное число. Имеем а=5; 2k=-18 <=> k=—9; с=9 =>
![]()
![]()
Ответ: {3; 3/5}
Пример 3. Решить уравнение х² - 4х +4 - 0.
Решение.
a=1; 2k=-4 <=> k=-2; c=4 =>
![]()
<=> x1 = х2 = 2.
Ответ: {2}.
Замечание. Уравнение х²-4х + 4 = 0 можно решать без использования формул для решения квадратного уравнения. Заметив, что х² -4х + 4 = (х-2)², получаем х² -4х + 4 = 0 <=> (х-2)² = 0 <=> х-2 = 0 <=> х = 2.
Пример 4. Решить уравнение х² + х + 1 = 0.
Решение.
х²+х + 1 = 0, D = 1²- 4·1·1 = 1- 4=-3 уравнение не имеет действительных корней.
Ответ: ∅.
Неполные квадратные уравнения
Если второй коэффициент b или свободный член с равны нулю, то квадратное уравнение ах² + Ьх + с = 0 называется неполным. Для отыскания корней неполного квадратного уравнения обычно не пользуются формулами для нахождения корней полного квадратного уравнения, т. к. неполные квадратные уравнения проще решать методом разложения их левой части на линейные множители.
Итак, рассмотрим решение уравнения ах² + Ьх + с = О, когда 1) с=0; 2) Ь=0; 3) Ь=с=0.
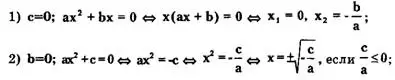
если c/a > 0, то уравнение не имеет действительных корней.
3) Ь=с=0; ах² = 0 <=> х1 = х2 = 0 (а≠0).
Пример 1. Решить уравнение Зх² -8х = 0.
Решение.
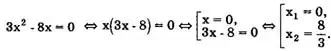
Ответ: {0; 8/3}
Пример 2. Решить уравнение 5х² -125 = О.
Решение.
![]()
![]()
Ответ: {-5;5}.
Пример 3. Решить уравнение Зх² +11 = 0.
Решение.
![]()
Ответ: ∅.






