Линейным уравнением с одной переменной х называется уравнение вида а•х=b, где а и b — заданные числа; а называется коэффициентом при переменной х, b — свободным членом. Для линейного уравнения а•х=b возможны три случая:
1) а≠0, тогда а•х=b<=> х=b/a — единственный корень уравнения;
2) а=0, b=0, тогда уравнение а•х=b принимает вид 0•х=0, что верно при любом х, т. е. корнем уравнения является любое действительное число;
3) а=0, b≠0, тогда уравнение а•х=b принимает вид О•х=Ь, оно не имеет корней.
Пример 1.
![]()
Ответ: {-5}.
Уравнения, приводимые к линейным
Уравнения вида
![]()
![]()
приводятся (сводятся) к линейным путем преобразований. Запишем решения этих уравнений:
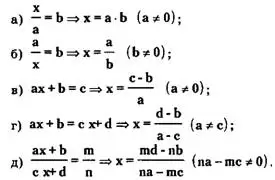
Пример 2. Решить уравнение
![]()
Решение.
![]()
Ответ: {2/3}.
Пример 3. Решить уравнение
![]()
Решение.
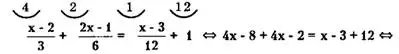
![]()
Ответ: {19/7}






