Этод метод заключается в следующем:
1) приравниваются к нулю выражения, стоящие под знаком модуля;
2) полученные значения откладываются на числовой прямой, которая при этом разбивается на интервалы (промежутки), в каждом из которых свой знак под модульного выражения;
3) решаются полученные уравнения в каждом из интервалов.
На практике метод интервалов обычно применяется тогда, когда уравнение содержит более одного модуля.
Рассмотрим применение метода интервалов на конкретных примерах.
Пример 1. Решить уравнение |х + 2| + |х-4| = 5х-20.
Решение.
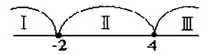х + 2 = 0<=>х = -2; х-4 = 0 <=> х = 4. Наносим на числовую прямую точки х = -2 и х = 4. Эти точки разбивают прямую на три интервала (промежутка), в каждом из которых свой знак подмодульного выражения.
Обозначим эти интервалы I, II, III, где
I: х<-2; II: -2 ≤ х ≤ 4; III: х>4 (рис. 1).
Для интервала I имеем: |х+ 2| = -(х+ 2) =-х-2;
|х-4| = -(х-4) = -х + 4.
Отсюда получаем решение уравнения в I интервале:
-х-2-х + 4 = 5х-20 <=> -2 + 4 + 20 = х + х + 5х <=> 22 = 7х <=> х = 22/7.
Однако значение х = 22/7 не принадлежит I интервалу, где x<-2, иначе говоря, 22/7 ∉ (-∞;-2), отсюда в I интервале исходное уравнение |х + 2| + |х - 4| = 5х - 20 решений не имеет.
Для II интервала |х + 2| = х + 2, |х-4| =-(х-4) =-х + 4 => исходное уравнение имеет вид х + 2 + (-х + 4)=5х-20=> 5x = 2 + 4+26 <=> x=26/5.
Однако 26/5 не входит в интервал -2 ≤ х ≤ 4, значит, во II интервале исходное уравнение решений не имеет.
Для ІII интервала |х + 2| = х + 2, |х-4| = х- 4 => исходное уравнение имеет вид: х + 2 + х- 4 = 5х-20 <=> 2 - 4 + 20 = -х - х + 5х <=> <=> 18 = Зх <=> х = 6. Т. к. 6 входит в интервал х>4, то х = 6 является решением исходного уравнения.
Ответ: {6}.
Замечание. Решение примера 1 можно записать в следующей форме, применяя понятие совокупности смешанных систем, т. е. систем, содержащих уравнения и неравенства.
|х + 2| + |х-4| = 5х-20.
Имеем три интервала I: х < -2; II: - 2 ≤ х ≤ 4; III: х > 4. Отсюда, в зависимости от того, в каком интервале мы ищем решение, исходное уравнение равносильно совокупности следующих смешанных систем:
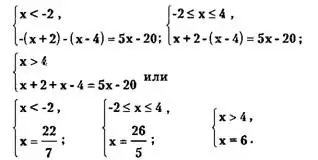
Первая и вторая системы решений не имеют (это означает, что в I и во II интервале решений нет), т.к. 22/7 ∉ (-∞;-2), 26/5 ∉ [-2;4], а третья система имеет решение х = 6.
Ответ: {6}.
Пример 2. Решить уравнение |х-2| + |х + 2| = 4.
Решение.
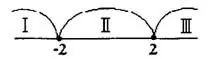х - 2 = 0 <=> х = 2; х + 2 = 0 <=> х = -2. Имеем три интервала (рис. 2):
І: хє(-∞;-2); II: х є [-2;2]; III: хє(2;∞).
В I интервале |х-2| = -(х-2), |х + 2| = -(х + 2).
Во II интервале |х-2| = -(х-2), |х + 2| = х + 2.
В III интервале |х-2| = х-2, |х + 2| = х + 2.
Отсюда получаем совокупность, состоящую из трех смешанных систем:
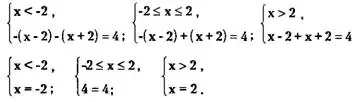
Первая и третья системы решений не имеют, поскольку -2 ∉ (-∞;-2), 2 ∉ (2;∞). Т. к. 4=4 — это тождество, то для второй системы любое х є [-2;2] является решением, т. е. решением второй системы является весь отрезок [—2;2].
Ответ: х є [-2;2].
