При решении уравнений, содержащих переменную под знаком модуля, чаще всего применяют следующие методы:
а) раскрытие модуля по определению;
б) возведение обеих частей уравнения в квадрат;
в) метод интервалов (промежутков).
Вспомним определение модуля:
![]()
Отметим следующие свойства модуля, которые нередко используются на практике:
![]()
![]()
Прежде чем начать решать уравнение с модулем, заметим, что уравнение |f(x)| = а равносильно совокупности уравнений
![]()
если а ≥ 0. Если же а < 0, то уравнение |f(x)| = a решений не имеет.
Пример 1. Решить уравнение |2х-1| = 5.
Решение.
![]()
Ответ: {3;-2}.
Пример 2. Решить уравнение |х + 2| = 0.
Решение.
|х + 2| = 0 <=> х + 2 = 0 <=> х = -2.
Ответ: {-2}.
Пример 3. Решить уравнение |2х + 5| = -1.
Решение.
|2х + 5| = -1 <=> х є ∅ , так как из определения модуля следует,
что |f(x)| ≥ 0 для любого х из области определения функции f(x).
Ответ: ∅.
Пример 4. Решить уравнение |х +1| = 2х -1.
Решение.
Рассмотрим два случая, когда подмодульное выражение (х + 1) неотрицательно и когда отрицательно. При х + 1 ≥ 0=> =>|х + 1| = х + 1. При х + 1 < 0 =>|х + 1| = -(х + 1). Отсюда исходное уравнение эквивалентно совокупности двух смешанных систем:
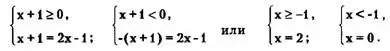
Первая система имеет решение х=2.
Вторая система решений не имеет, т. к. 0 ∉ (-∞;-1).
Ответ: {2}.
Пример 5. Решить уравнение |2х -1| = |х - l|.
Решение.
Исходное уравнение с двумя модулями можно решать методом интервалов, который рассмотрен ниже, однако для данного уравнения быстрее всего приводит к цели способ возведения обе¬их частей уравнения в квадрат, с учетом того что |f(x)|² = (f(x))².
Имеем
|2х-1| = |х-1| <=> |2х- 1|² = |х -1|² <=> (2х-1)² = (х - 1)² <=> 4х² - 4х +1 = х² - 2х +1 <=> Зх² - 2х = 0 <=> х(3х - 2) = 0 <=> x₁=0, x₂=2/3.
Ответ: {0; 2/3}.
Уравнения, содержащие переменную под знаком модуля






