Метод введения новой переменной был использован ранее при решении трехчленных уравнений, однако этот метод с успехом применяется и при решении многих других уравнений, где возможна и полезна замена переменной. Для закрепления этого метода рассмотрим несколько примеров.
Пример 1. Решить уравнение (х² + х)² - 8(х² + х) + 12 = 0.
Решение.
Положив х² + х = t, получим уравнение t² - 8t +12 = 0, откуда находим t₁ =2; t₂ = 6. Теперь задача свелась к решению совокупности уравнений х² + х = 2; х² + х = 6, то есть
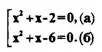
Уравнение (а) имеет корни x₁=-2, х₂=1; уравнение (б) имеет корни х₃ = -3, х₄ = 2.
Ответ: {-2;1;-3;2}.
Пример 2. Решить уравнение
![]()
Решение.
Замена ![]()
приводит исходное уравнение к квадратному t²-5t + 6 = 0, корни которого t₁=2, t₂=3. Взяв t₁=2 =>
![]()
Взяв t₂ =3 => ![]()
Ответ: ![]()
Пример 3. Решить уравнение
![]()
Решение.
Замена х² + х + 1 = t приводит исходное уравнение к такому:
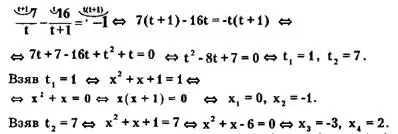
Ответ: {0; -1; -3; 2}
Пример 4. Решить уравнение
![]()
Решение.
Положим ![]()
Тогда ![]()
=х² + х⁻² + 2 => х² + х⁻² = t²-2. Исходное уравнение записывается в виде
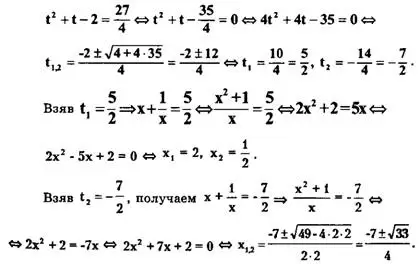
Ответ: ![]()
Пример 5. Решить уравнение (х + 3)⁴ + (х + 5)⁴ = 16.
Решение.
Уравнения вида ![]()
решаются с помощью замены ![]()
(с — среднее арифметическое чисел а и b). Для уравнения (х + З)⁴ + (х + 5)⁴ = 16
с = (3+5)/2 = 4 => делаем замену t = x + 4 =>
=> x = t - 4, x + 3 = t - 4 + 3 = t - 1, x + 5 = t- 4 + 5 = t + 1 => исходное уравнение записывается в виде (t-1)⁴ +(t + l)⁴ = 16. Применяя треугольник Паскаля, получаем
t⁴-4t³ + 6t²-4t +1 + t⁴ + 4t³ + 6t² + 4t +1 = 16 <=>
<=> 2t⁴ + 12t² + 2 = 16 <=> 2t⁴ + 12t² -14 = 0 <=> t⁴ + 6t² - 7 = 0.
Решая это биквадратное уравнение, получаем t₁ =1, t₂ = -1. Взяв t₁ = 1 => х + 4 = 1 <=> х = -4 + 1 = -3. Взяв t₂ = -1 => х + 4 = -1 <=> х = -4 -1 = -5 .
Ответ: {-3;-5}.
Пример 6. Решить уравнение Зх⁴ - 2х³ - 9х² - 4х + 12 = 0.
Решение.
В данном уравнении отношение первого коэффициента к свободному члену и квадрата второго коэффициента к квадрату предпоследнего равны между собой, то есть
![]()
Такие уравнения называются возвратными.
В общем случае уравнение вида ах⁴ + bх³ + сх² + dx + m = 0 называется возвратным, если
выполнено условие
![]()
Поскольку х=0 не является решением возвратного уравнения, то можно разделить обе части уравнения на х² и после замены переменных получить квадратное уравнение. Разделив исходное уравнение на х², получаем
![]()
Группируя слагаемые, имеем
![]()
Положив ![]()
имеем
![]()
Таким образом, приходим к уравнению
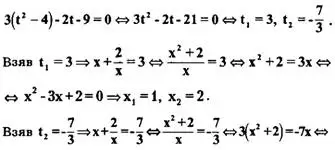
<=>Зх² +7х + 6 = 0. Т. к. дискриминант этого уравнения D=7²-4·3·6=49-72 = -23 < 0 , то оно действительных корней не имеет.
Ответ: {1;2}.
Решение рациональных и дробно-рациональных уравнений методом введения новой переменной






