Рассмотрим решение некоторых неполных рациональных уравнений высших степеней, у которых свободный член равен нулю. У подобного рода уравнений х=0 всегда является корнем. После вынесения х за скобки в скобках может получиться множитель, приравнивая нулю который, получаем уравнение степени на единицу меньше исходного, которое нередко удается легко решить.
Замечание. Иногда нужно выносить за скобки не х, а хⁿ где n > 1 (n ∈ N).
Пример 1. Решить уравнение х³ - х = 0.
Решение.
![]()
![]()
Ответ: {0;1;-1}.
Пример 2. Решить уравнение х³ -5х² +6х = 0.
Решение.
![]()
![]()
Ответ: {0;2;3}.
Пример 3. Решить уравнение 2х³+4х² =0.
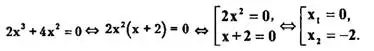
Ответ: {0;-2}.
Пример 4. Решить уравнение х⁴ + 9х² = 0.
Решение.
![]()
Ответ: {0}.
Пример 5. Решить уравнение x⁴ + 27х = 0.
Решение.
![]()
Ответ: {0;-3}.
Пример 6. Решить уравнение х⁶ -4х⁵ + 3х⁴ =0.
Решение.
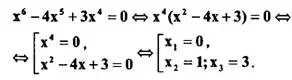
Ответ: {0;1;3}.
Пример 7. Решить уравнение х¹⁴- 7х = 0.
Решение.
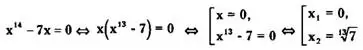
Ответ: ![]()
Решение некоторых неполных рациональных уравнений высших степеней






