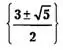Симметрические уравнения третьей степени
Рациональное уравнение третьей степени называется симметрическим, если оно имеет вид:
ах³ + bх² + bх + а = 0, (а≠0).
Для решения этого уравнения преобразуем многочлен, стоящий в левой части уравнения, используя разложение многочлена на множители. Имеем следующую цепочку тождественных преобразований:
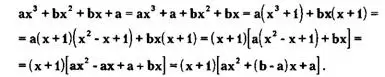
Отсюда получаем
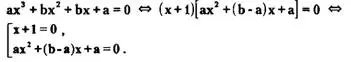
Получили совокупность уравнений, эквивалентную исходному кубическому уравнению. Решение полученной совокупности легко находится, поскольку эта совокупность содержит линейное и квадратное уравнения.
Пример. Решить уравнение х³ + 9х² + 9х + 1 = 0.
Решение.
Преобразуем левую часть уравнения:
х³ + 9х² + 9х + 1 = х³ +1 + 9х² +9х = (х + 1)(х² - x + 1) + 9x(x + 1) = (х +1)(x² - х + 1 + 9х) = (х + 1)(x² + 8x + 1).
Отсюда
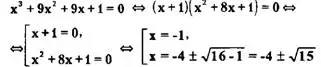
Ответ: ![]()
Симметрические уравнения четвертой степени
Рациональное уравнение четвертой степени называется симметрическим, если оно имеет вид
ax⁴ + bх³ + cх² + bх + а = 0, (а≠0).
Так как а≠0, то, разделив обе части на а, получаем равносильное уравнение
![]()
Сгруппировав первый член с последним и второй с четвертым, получаем
![]()
Заметим, что
![]()
Отсюда получаем цепочку тождественных преобразований:
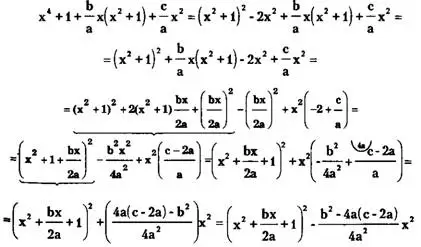
Отсюда при а≠0 имеем
![]()
Последнее уравнение нетрудно решить, так как его решение сводится к решению более простых уравнений. Рассмотрим пример.
Пример. Решить уравнение x⁴ - 2x³ - x² - 2x + 1=0
Решение.
Преобразуем левую часть исходного уравнения:
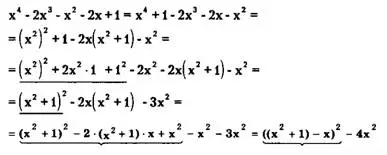
Таким образом,
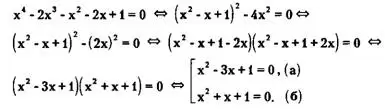
Уравнение (а) совокупности уравнений имеет корни x₁ и х₂:
![]()
Уравнение (б) действительных корней не имеет, т. к. его дискриминант D = 1²- 4∙1∙1 = 1- 4 =-3<0.
Ответ: