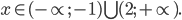Обобщенный метод интервалов
Пусть требуется решить неравенство
где
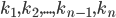 - целые положительные числа;
- целые положительные числа;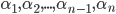 — действительные числа, среди которых
— действительные числа, среди которыхнет равных и такие, что
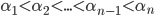 . Неравенства подобного типа решают с применением обобщенного метода интервалов. В основе этого метода лежит следующее свойство двучлена
. Неравенства подобного типа решают с применением обобщенного метода интервалов. В основе этого метода лежит следующее свойство двучлена 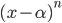 : точка
: точка  делит числовую ось на две части причем если
делит числовую ось на две части причем если 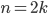 (n — четное), то выражение
(n — четное), то выражение 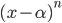 справа и слева от точки
справа и слева от точки  сохраняет положительный знак; если
сохраняет положительный знак; если 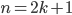 (n — нечетное число), то выражение
(n — нечетное число), то выражение 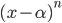 справа от точки
справа от точки  положительно, а слева от точки
положительно, а слева от точки  отрицательно.
отрицательно. Для решения неравенства
обобщенным методом интервалов на числовую ось наносим числа
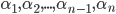 ; в промежутке справа от наибольшего из них ставим знак «плюс», а затем, двигаясь справа налево, при переходе через очередное число
; в промежутке справа от наибольшего из них ставим знак «плюс», а затем, двигаясь справа налево, при переходе через очередное число 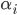 меняем знак, если
меняем знак, если 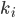 — нечетное число, и сохраняем знак, если
— нечетное число, и сохраняем знак, если 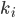 — четное число.
— четное число.Замечание 1. Если встречаются выражения
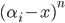 , то справа от наибольшего из
, то справа от наибольшего из 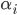 не обязательно будет знак «+». В этом случае лучше всего определить знак левой части неравенства в каком-либо из интервалов, а затем поставить знаки в каждом из интервалов с учетом изложенных выше соображений.
не обязательно будет знак «+». В этом случае лучше всего определить знак левой части неравенства в каком-либо из интервалов, а затем поставить знаки в каждом из интервалов с учетом изложенных выше соображений.Замечание 2. Приведенные выше рассуждения справедливы и для неравенств вида
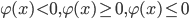 , где
, где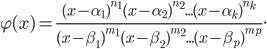
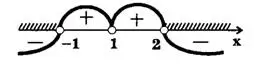
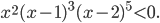 Решение. Отмечаем на числовой прямой точки
Решение. Отмечаем на числовой прямой точки 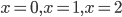 (рис.1). Проводим через эти точки «кривую знаков» с учетом того, что слева и справа от точки
(рис.1). Проводим через эти точки «кривую знаков» с учетом того, что слева и справа от точки  будет один и тот же знак « + », так
будет один и тот же знак « + », таккак в выражении
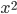 показатель степени (число 2) есть число четное. В окрестности точек
показатель степени (число 2) есть число четное. В окрестности точек 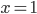 и
и 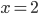 знаки в соседних промежутках чередуются, так как в выражениях
знаки в соседних промежутках чередуются, так как в выражениях 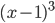 и
и 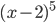 показатели степеней (числа 3 и 5) нечетные.
показатели степеней (числа 3 и 5) нечетные.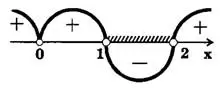
Множество, дающее решение исходного неравенства, заштриховано на рис.1. Это интервал (1;2).
Ответ: 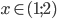 .
.
Пример 2. Решить неравенство 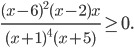
Решение. Наносим на числовую прямую точки 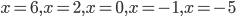 . Точки
. Точки 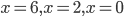 отмечаем темными кружками, а точки
отмечаем темными кружками, а точки 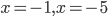 светлыми (рис.2). Проведя «кривую знаков» с учетом того, что в окрестности точек
светлыми (рис.2). Проведя «кривую знаков» с учетом того, что в окрестности точек 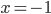 и
и 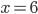 левая часть неравенства сохраняет знак (т. к. в выражениях
левая часть неравенства сохраняет знак (т. к. в выражениях 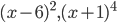 показатели степеней есть четные числа), получаем решение
показатели степеней есть четные числа), получаем решение ![x\in (-5;-1)\bigcup (-1;0]\bigcup [2;6]\bigcup [6;+\propto)=(-5;-1)\bigcup (-1;0]\bigcup [2;+\propto).](https://math-helper.ru/wp-content/plugins/latex/cache/tex_3645f646574a06a502c2bbaa336bc9f9.gif)

Это множество на рис.2 заштриховано.
Ответ: ![x\in (-5;-1)\bigcup (-1;0]\bigcup [2;+\propto).](https://math-helper.ru/wp-content/plugins/latex/cache/tex_ddbc9b406294346f5bb58c1743ee547b.gif)
Пример 3. Решить неравенство 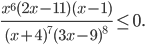
Решение.
Наносим точки 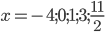 на числовую ось. С помощью «кривой знаков» получаем решение, заштрихованное на рис.3. Заметим, что точка
на числовую ось. С помощью «кривой знаков» получаем решение, заштрихованное на рис.3. Заметим, что точка  входит в множество решений, т. к. при
входит в множество решений, т. к. при  получаем
получаем 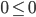 .
.

Ответ: ![x\in (-\propto ;-4)\bigcup\left\{0 \right\}{0} \bigcup [1;3)\bigcup \left(3;\frac{11}{2} \right].](https://math-helper.ru/wp-content/plugins/latex/cache/tex_3e04195003ca36abad04d14a4f2a2bd7.gif)
Пример 4. Решить неравенство 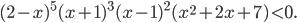 Решение. Наносим точки
Решение. Наносим точки 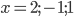 на числовую ось (поскольку дискриминант квадратного трехчлена
на числовую ось (поскольку дискриминант квадратного трехчлена 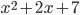 :
: 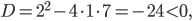 то для всех
то для всех  и, значит, парабола
и, значит, парабола 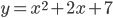 не пересекает ось Ох). С помощью «кривой знаков» получаем решение, заштрихованное на рис.4.
не пересекает ось Ох). С помощью «кривой знаков» получаем решение, заштрихованное на рис.4.
Ответ: