Метод замены переменной при решении рациональных неравенств
Многие неравенства удобно решать, применяя метод замены переменной (метод подстановки).
Пример 1. Решить неравенство  . Решение. Сделав замену переменной
. Решение. Сделав замену переменной 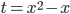 , получаем
, получаем  . Корни уравнения
. Корни уравнения 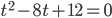 есть
есть 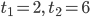 .
Отсюда
.
Отсюда  Поскольку
Поскольку 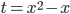 , то получаем
, то получаем
Решаем неравенство (a):
Решаем неравенство (b):

Изобразим полученные множества с помощью двух координатных прямых (рис.1). Из рис.1 видим, что решением исходного неравенства является объединение множеств (-2;-1),(2;3).
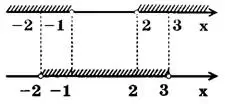
Рис.1
Ответ: 
Пример 2. Решить неравенство  Решение.
Решение.
Обозначив  , получаем из исходного неравенства
, получаем из исходного неравенства  Отсюда исходное неравенство равносильно следующему неравенству:
Отсюда исходное неравенство равносильно следующему неравенству:
( для любого
 , поскольку дискриминант квадратного трехчлена
, поскольку дискриминант квадратного трехчлена 
Ответ:







