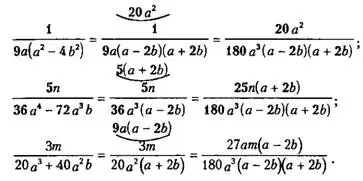Приведение рациональных дробей к общему знаменателю
Общим знаменателем двух или нескольких рациональных Дробей называется целое рациональное выражение, которое делится на знаменатель каждой дроби.
Например, общим знаменателем дробей
![]()
является многочлен (x - 1)(2х + 1), однако не только он, но и многочлены 2(х-1)(2х + 1), 7х(х - 1)(2х + 1), 9х²(х-1)³(2х+1)² и Т. Д. Предпочтительнее взять наименьший общий знаменатель — такой простейший общий знаменатель, что любой другой общий знаменатель делится на этот простейший. Наименьшим общим
знаменателем дробей
![]()
является (х - 1)(2х + 1).
Можно записать:
![]()
Приведение исходных дробей к наименьшему общему знаменателю (в дальнейшем будем называть его просто общим знаменателем) было достигнуто умножением числителя и знаменателя первой дроби на (2х +1), а числителя и знаменателя второй дроби на (х-1). Многочлены (2х + 1) и (х-1) называют дополнительными множителями для первой и второй дробей соответственно. Таким образом, дополнительный множитель для данной дроби равен частному от деления общего знаменателя на знаменатель данной дроби.
Для того чтобы несколько рациональных дробей привести к общему знаменателю, необходимо:
1) разложить знаменатель каждой дроби на множители, если это возможно;
2) составить общий знаменатель, включив в него в качестве сомножителей все различные множители, полученные в пункте 1); если некоторый множитель имеется в нескольких разложениях, то он берется с показателем степени, равным наибольшему из имеющихся;
3) определить дополнительные множители для каждой из дробей, для чего общий знаменатель разделить на знаменатель каждой дроби;
4) умножить числитель и знаменатель каждой дроби на дополнительный множитель.
Пример. Привести дроби к общему знаменателю.
![]()
Решение.
![]()
![]()
Наименьшее общее кратное чисел 9, 36, 20 есть число 180. Отсюда общий знаменатель имеет вид 180·а³(а- 2b)(а + 2b). Дополнительные множители: 20а², 5(а + 2b), 9а(а - 2b),— для первой, второй и третьей дробей соответственно.
Окончательно получаем: