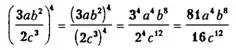Сложение и вычитание рациональных дробей. Умножение и деление рациональных дробей. Возведение рациональных дробей в степень

Сумма (разность) двух рациональных дробей с одинаковыми знаменателями тождественно равна дроби с тем же знаменателем и с числителем, равным сумме (разности) числителей исходных дробей:
![]()
Пример 1.
![]()
Пример 2.
![]()
x≠y.
При сложении (или вычитании) рациональных дробей с разными знаменателями нужно привести дроби к общему знаменателю и выполнить сложение (или вычитание) дробей с общим знаменателем:
![]()
где m — дополнительный множитель для первой дроби, n — дополнительный множитель для
второй дроби, S — общий знаменатель.
Замечание. Приведенные правила справедливы для любого конечного числа дробей.
Пример 3.
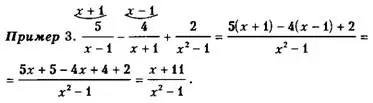
Пример 4. Упростить выражение
![]()
Решение.
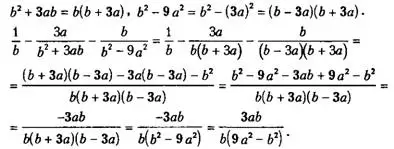
Ответ:
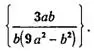
Умножение и деление рациональных дробей
Произведение двух рациональных дробей тождественно равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей перемножаемых дробей:
![]()
Это правило распространяется на произведение любого конечного числа дробей.
Частное от деления двух рациональных дробей тождественно равно дроби, числитель которой равен произведению числителя первой дроби на знаменатель второй дроби, а знаменатель — произведению знаменателя первой дроби на числитель второй дроби:
![]()
Если дробь умножается или делится не на дробь, а на многочлен R(x), то указанные выше правила остаются в силе, но многочлен R(x) необходимо представить в виде
![]()
На практике при умножении или делении рациональных дробей обычно предварительно разлагают на множители числители и знаменатели исходных дробей (если это возможно).
Пример 1. Упростить выражение
![]()
Решение.
![]()
![]()
![]()
Ответ:
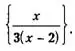
Пример 2. Упростить выражение
![]()
Решение.
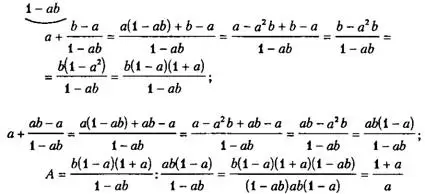
Ответ:
![]()
Возведение рациональных дробей в степень
Степень рациональной дроби тождественно равна дроби, у которой числитель есть степень числителя, а знаменатель — степень знаменателя:
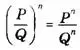
Например:
![]()