Равносильность уравнений
Напомним, что если из истинности высказывания А следует истинность высказывания В, то употребляют знак логического следования =>, т. е. А =>В (читается: из А следует В).
Если А=>В и В=>А,то такие высказывания называются равносильными (эквивалентными). Записывается это так: А <=> В (читается: А эквивалентно В, А равносильно В).
Два уравнения называются равносильными (эквивалентны¬ми), если множества их решений (корней) совпадают, т. е. это такие уравнения, которые имеют одни и те же корни. Равносильными считаются и уравнения, каждое из которых не имеет корней.
Например, уравнения х+1=7 и х+4=10 равносильны, т. к. каждое из них имеет единственный корень — число 6. Равносильны и уравнения х²=-4 и Зх²+5=0 (в области действительных чисел), т. к. ни одно из них не имеет корней.
Уравнения х—8=1 и х²=81 не равносильны, т.к. уравнение х—8=1 имеет только один корень х=9, тогда как уравнение х² = 81 имеет два корня: x1 = 9 и х2 = -9.
Преобразования, при которых уравнение переходит в равносильное ему уравнение
1) Если в уравнении поменять местами левую и правую части, то получится уравнение, равносильное данному. Например, х + 4 = 2х + 9<=> 2х + 9 = х + 4 .
2) Если в уравнении какое-нибудь слагаемое перенести из одной части в другую, изменив его знак на противоположный, то получится уравнение, равносильное данному. Например, 2х +7=х-3<=>2х-х=-7-3.
3) Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному. Например, уравнение
![]()
равносильно уравнению х+1=4х (уравнение х+1=4х получено из уравнения
![]()
умножением обеих частей на число 4).
4) Если к обеим частям уравнения прибавить или вычесть одно и то же число, то получится уравнение, равносильное данному. Например, х + 2=5х<=>х + 2 + 7 = 5х + 7; 5х + 2 = 0<=>5х+ 2- 2 = 0- 2.
5) Если к обеим частям уравнения прибавить или вычесть любую функцию, то получится уравнение, равносильное данному при условии, что области определения полученного и данного уравнений совпадают. Например, х = 2<=>х + х²=2 + х²; х³ + 5х = 8 + 5х <=> х³ = 8
Совокупность уравнений
Несколько уравнений с одной переменной образуют совокупность уравнений, если находятся все такие значения переменной, каждое из которых удовлетворяет по крайней мере одному из заданных уравнений. Уравнения, образующие совокупность уравнений, записываются в столбик с помощью квадратной скобки, например
![]()
или с помощью знака «;» (точка с запятой), например х + 3 = 2х - 7; х² - 5х + 6 = 0.
Решением совокупности уравнений является объединение множеств корней уравнений, составляющих данную совокупность.
Например, уравнение 2х(х-1)(х²-7х + 12) = 0 равносильно
совокупности уравнений:
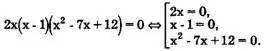
Решая каждое из уравнений совокупности, получаем корни исходного уравнения: x1 = 0; х2 = 1; х3 = 3; х4 = 4.






