Рассмотрим более сложные иррациональные неравенства.
Иррациональное неравенство  равносильно системе неравенств,
т. е. Иррациональное неравенство равносильно совокупности двух систем неравенств,
равносильно системе неравенств,
т. е. Иррациональное неравенство равносильно совокупности двух систем неравенств,
т. е.
Замечание. Если рассмотреть неравенства  и
и  , то эти неравенства эквивалентны приведенной выше системе неравенств и совокупности двух систем неравенств, в которых знаки строгих неравенств везде заменены на знаки нестрогих, кроме неравенства
, то эти неравенства эквивалентны приведенной выше системе неравенств и совокупности двух систем неравенств, в которых знаки строгих неравенств везде заменены на знаки нестрогих, кроме неравенства  , которое остается неизменным. Пример 1. Решить неравенство
, которое остается неизменным. Пример 1. Решить неравенство  .
.
Решение.
Неравенство (c) равносильно следующему:
Множества, полученные при решении неравенств (а), (b), (c), необходимо пересечь. Для этого, во избежание ошибок, лучше всего начертить три оси и нанести на каждую из осей полученные множества решений.
Полученные множества пересекаются при (рис.1).
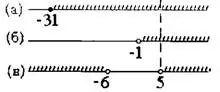
Ответ:  .
.
Пример 2. Решить неравенство  . Решение.
. Решение.
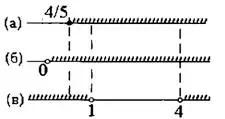
Пересекая множества, полученные при решении неравенств (а), (b), (c) (рис.2), получаем решение исходного неравенства:  .
.
Ответ:  .
.
Пример 3. Решить неравенство .
Решение.
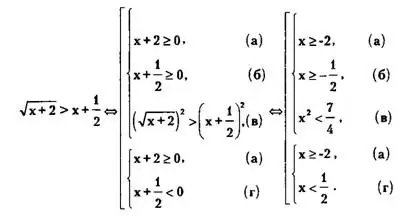
Решая неравенство (в), получаем

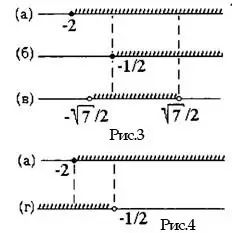
Пересекая множества, полученные при решении неравенств (а), (б), (в) (рис.3), получаем
 Пересекая множества, полученные при решении неравенств (а) и (г) (рис.4), получаем
Пересекая множества, полученные при решении неравенств (а) и (г) (рис.4), получаем  Решение исходного неравенства есть объединение множеств:
Решение исходного неравенства есть объединение множеств:

Пример 4. Решить неравенство
Решение.
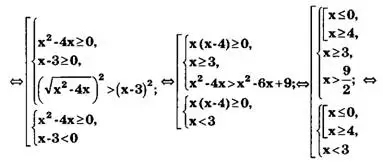
Ответ:
![x\in \left (-\infty ;0 \right ]\bigcup \left ( \frac{9}{2};\infty \right ).](https://math-helper.ru/wp-content/plugins/latex/cache/tex_444918defae7d99100169a3977d1e47a.gif)






