Числовой последовательностью называется функция, определенная на множестве натуральных чисел (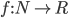 ,
, 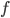 - функция натурального аргумента). Обозначается числовая последовательность обычно через
- функция натурального аргумента). Обозначается числовая последовательность обычно через 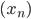 , где
, где 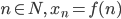 — n-й член последовательности. Формула
— n-й член последовательности. Формула 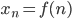 называется формулой общего члена последовательности
называется формулой общего члена последовательности 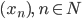 .
.
Примеры числовых последовательностей
Пример 1. Пусть числовая последовательность задана общим членом  . Это означает, что каждому натуральному числу
. Это означает, что каждому натуральному числу  соответствует определенный член последовательности
соответствует определенный член последовательности 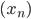 , т. е.
, т. е.  . Придавая
. Придавая  значения 1,2,3,..., получим последовательность
значения 1,2,3,..., получим последовательность 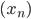 :
:  .
.
Пример 2. Для числовой последовательности  формула общего члена имеет вид
формула общего члена имеет вид  .
.
Пример 3. Пусть последовательность задана формулой  . Все члены последовательности с нечетными номерами равны -1, а с четными номерами равны 1:
. Все члены последовательности с нечетными номерами равны -1, а с четными номерами равны 1:  . Получаем последовательность -1;1;-1;1;-1;...
. Получаем последовательность -1;1;-1;1;-1;...
Пример 4. Формулой  задается последовательность, все члены которой равны 2: 2; 2; 2; 2; 2;
задается последовательность, все члены которой равны 2: 2; 2; 2; 2; 2;
Последовательность 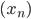 называется возрастающей, если каждый ее член, начиная со второго, больше предыдущего, т. е. если для всех . Пример возрастающей последовательности: 1; 3; 5; 7; 9;...; (2n-1);... .
называется возрастающей, если каждый ее член, начиная со второго, больше предыдущего, т. е. если для всех . Пример возрастающей последовательности: 1; 3; 5; 7; 9;...; (2n-1);... .
Последовательность 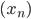 называется убывающей, если каждый ее член, начиная со второго, меньше предыдущего, т. е. если для всех
называется убывающей, если каждый ее член, начиная со второго, меньше предыдущего, т. е. если для всех  . Пример убывающей последовательности:
. Пример убывающей последовательности:  .
.
Понятие числовой последовательности






