Пример 1. Найти арифметическую прогрессию, если сумма её  первых членов
первых членов 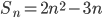 .
.
Решение.
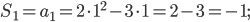
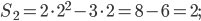
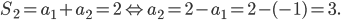
Отсюда 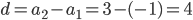 .
.
Ответ: 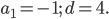
Пример 2. Найти десятый член арифметической прогрессии, если сумма ее  первых членов
первых членов 
Решение.

Ясно, что

Ответ: {55}.
Пример 3. В арифметической прогрессии 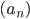
 Найти
Найти  .
.
Решение.

Ответ: {7}.
Пример 4. Найти сумму всех двузначных натуральных чисел, которые при делении на 4 дают в остатке 1.
Решение.
Имеем 
Найдем число  членов этой прогрессии из формулы
членов этой прогрессии из формулы 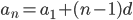 . Подставив
. Подставив  , получаем
, получаем

Отсюда 
Ответ: {1210}.
Пример 5. Решить уравнение 
Решение.
Имеем  .
.
С другой стороны,


Тогда по условию  Отсюда
Отсюда

Ответ: {1}.
Решение типовых задач на арифметическую прогрессию. Часть 2






